On the Outsized Importance of Learning Rates in Local Update Methods
Paper and Code
Jul 02, 2020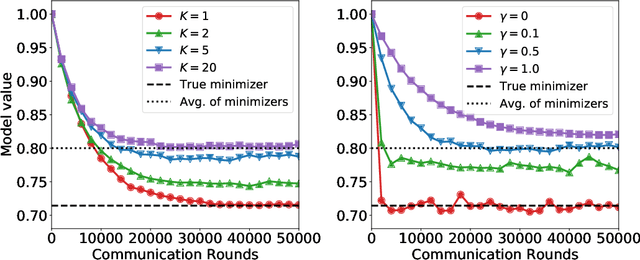

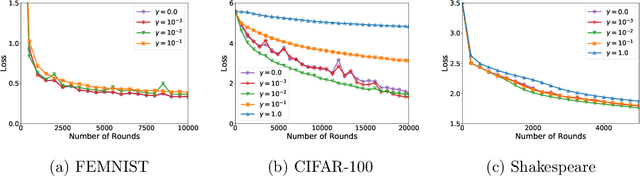
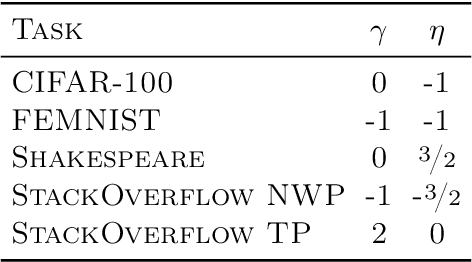
We study a family of algorithms, which we refer to as local update methods, that generalize many federated learning and meta-learning algorithms. We prove that for quadratic objectives, local update methods perform stochastic gradient descent on a surrogate loss function which we exactly characterize. We show that the choice of client learning rate controls the condition number of that surrogate loss, as well as the distance between the minimizers of the surrogate and true loss functions. We use this theory to derive novel convergence rates for federated averaging that showcase this trade-off between the condition number of the surrogate loss and its alignment with the true loss function. We validate our results empirically, showing that in communication-limited settings, proper learning rate tuning is often sufficient to reach near-optimal behavior. We also present a practical method for automatic learning rate decay in local update methods that helps reduce the need for learning rate tuning, and highlight its empirical performance on a variety of tasks and datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge