On the failure of variational score matching for VAE models
Paper and Code
Oct 24, 2022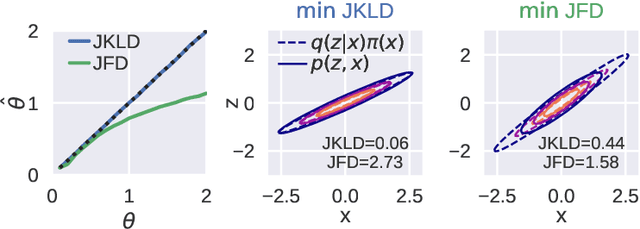
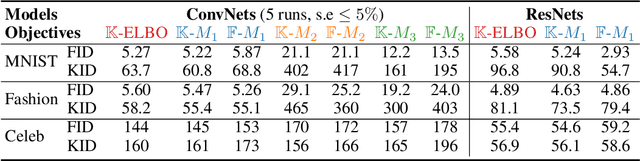
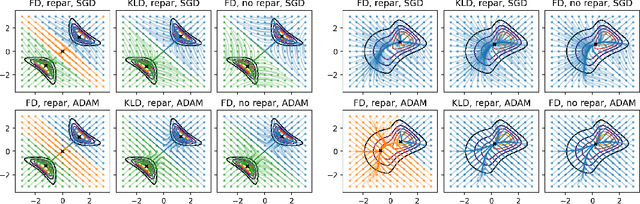
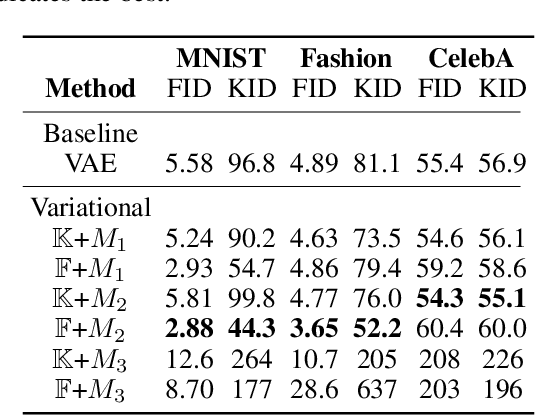
Score matching (SM) is a convenient method for training flexible probabilistic models, which is often preferred over the traditional maximum-likelihood (ML) approach. However, these models are less interpretable than normalized models; as such, training robustness is in general difficult to assess. We present a critical study of existing variational SM objectives, showing catastrophic failure on a wide range of datasets and network architectures. Our theoretical insights on the objectives emerge directly from their equivalent autoencoding losses when optimizing variational autoencoder (VAE) models. First, we show that in the Fisher autoencoder, SM produces far worse models than maximum-likelihood, and approximate inference by Fisher divergence can lead to low-density local optima. However, with important modifications, this objective reduces to a regularized autoencoding loss that resembles the evidence lower bound (ELBO). This analysis predicts that the modified SM algorithm should behave very similarly to ELBO on Gaussian VAEs. We then review two other FD-based objectives from the literature and show that they reduce to uninterpretable autoencoding losses, likely leading to poor performance. The experiments verify our theoretical predictions and suggest that only ELBO and the baseline objective robustly produce expected results, while previously proposed SM methods do not.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge