On the effectiveness of persistent homology
Paper and Code
Jun 21, 2022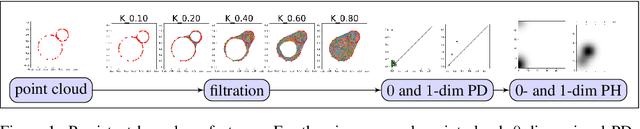

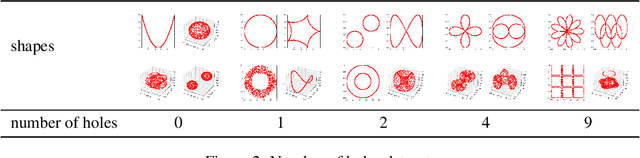
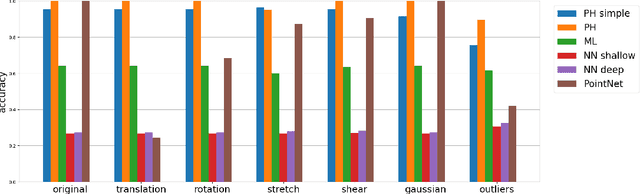
Persistent homology (PH) is one of the most popular methods in Topological Data Analysis. While PH has been used in many different types of applications, the reasons behind its success remain elusive. In particular, it is not known for which classes of problems it is most effective, or to what extent it can detect geometric or topological features. The goal of this work is to identify some types of problems on which PH performs well or even better than other methods in data analysis. We consider three fundamental shape-analysis tasks: the detection of the number of holes, curvature and convexity from 2D and 3D point clouds sampled from shapes. Experiments demonstrate that PH is successful in these tasks, outperforming several baselines, including PointNet, an architecture inspired precisely by the properties of point clouds. In addition, we observe that PH remains effective for limited computational resources and limited training data, as well as out-of-distribution test data, including various data transformations and noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge