On the Dynamics of Hopfield Neural Networks on Unit Quaternions
Paper and Code
Dec 13, 2021
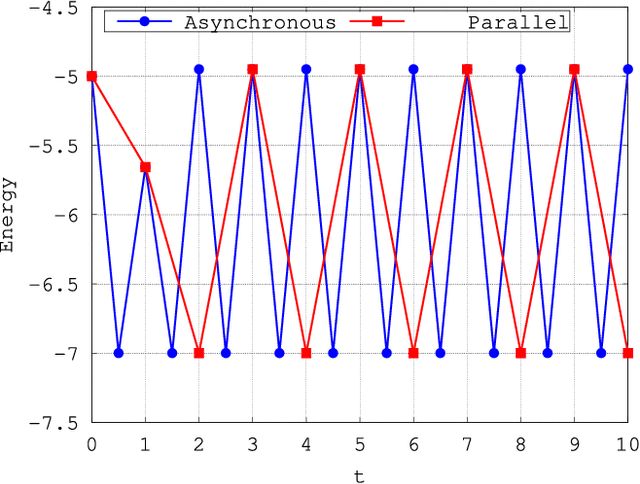
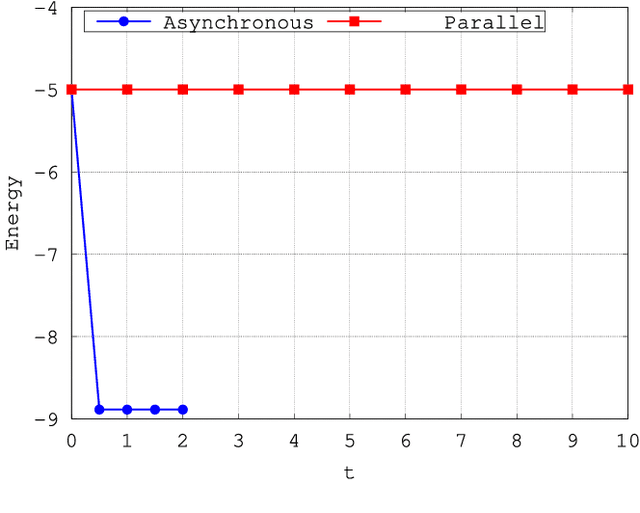

In this paper, we first address the dynamics of the elegant multi-valued quaternionic Hopfield neural network (MV-QHNN) proposed by Minemoto and collaborators. Contrary to what was expected, we show that the MV-QHNN, as well as one of its variation, does not always come to rest at an equilibrium state under the usual conditions. In fact, we provide simple examples in which the network yields a periodic sequence of quaternionic state vectors. Afterward, we turn our attention to the continuous-valued quaternionic Hopfield neural network (CV-QHNN), which can be derived from the MV-QHNN by means of a limit process. The CV-QHNN can be implemented more easily than the MV-QHNN model. Furthermore, the asynchronous CV-QHNN always settles down into an equilibrium state under the usual conditions. Theoretical issues are all illustrated by examples in this paper.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge