On the dice loss gradient and the ways to mimic it
Paper and Code
Apr 09, 2023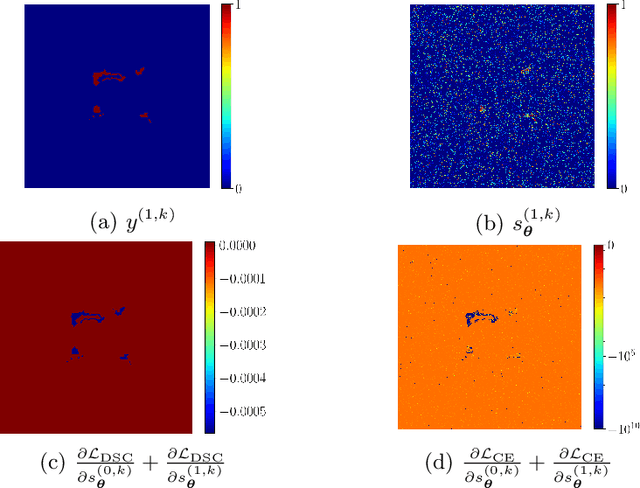
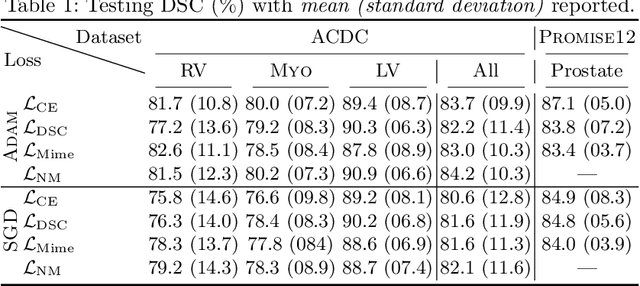
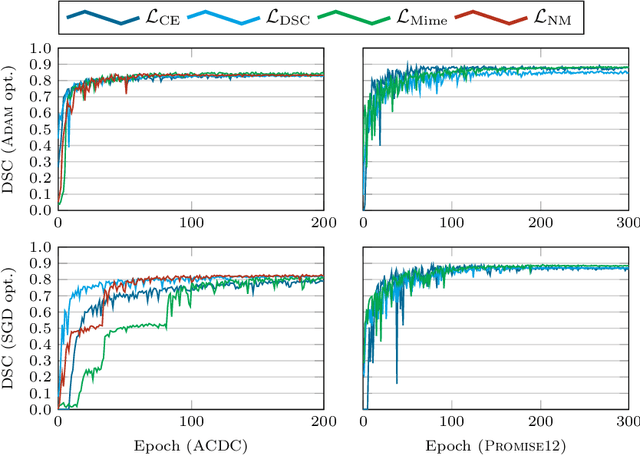
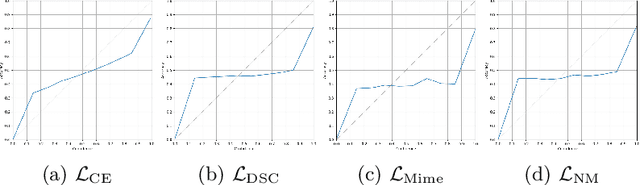
In the past few years, in the context of fully-supervised semantic segmentation, several losses -- such as cross-entropy and dice -- have emerged as de facto standards to supervise neural networks. The Dice loss is an interesting case, as it comes from the relaxation of the popular Dice coefficient; one of the main evaluation metric in medical imaging applications. In this paper, we first study theoretically the gradient of the dice loss, showing that concretely it is a weighted negative of the ground truth, with a very small dynamic range. This enables us, in the second part of this paper, to mimic the supervision of the dice loss, through a simple element-wise multiplication of the network output with a negative of the ground truth. This rather surprising result sheds light on the practical supervision performed by the dice loss during gradient descent. This can help the practitioner to understand and interpret results while guiding researchers when designing new losses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge