On the Computational Complexity of Multi-Agent Pathfinding on Directed Graphs
Paper and Code
Nov 11, 2019
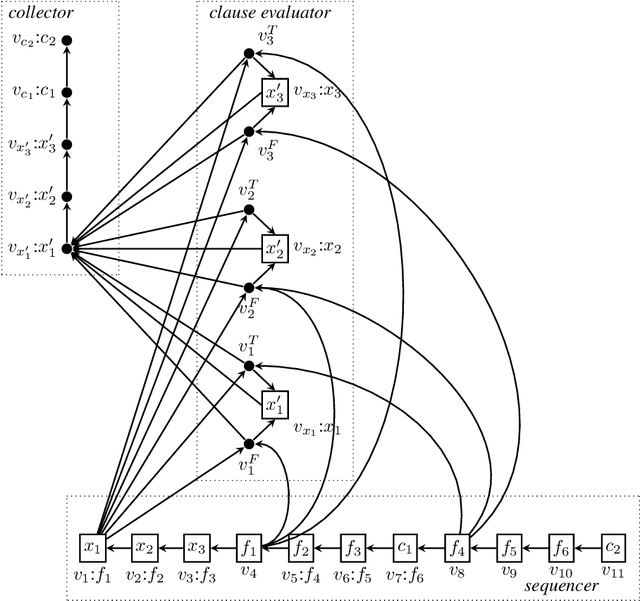
The determination of the computational complexity of multi-agent pathfinding on directed graphs has been an open problem for many years. For undirected graphs, solvability can be decided in polynomial time, as has been shown already in the eighties. Further, recently it has been shown that a special case on directed graphs is solvable in polynomial time. In this paper, we show that the problem is NP-hard in the general case. In addition, some upper bounds are proven.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge