On the Assessment of Benchmark Suites for Algorithm Comparison
Paper and Code
Apr 15, 2021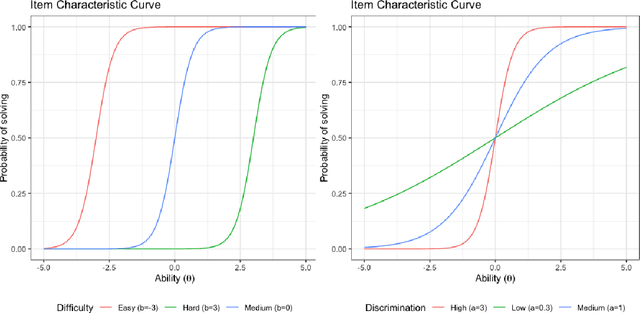
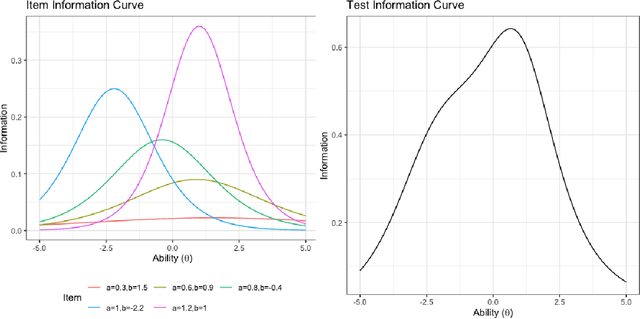
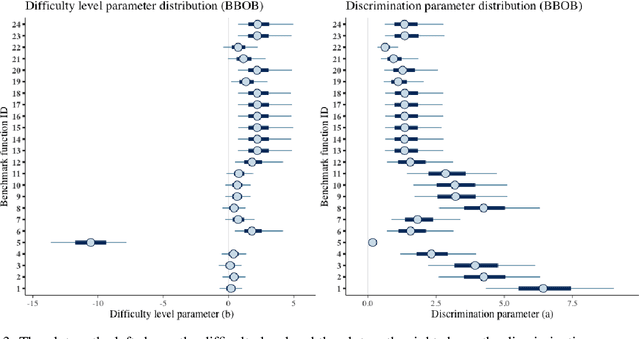
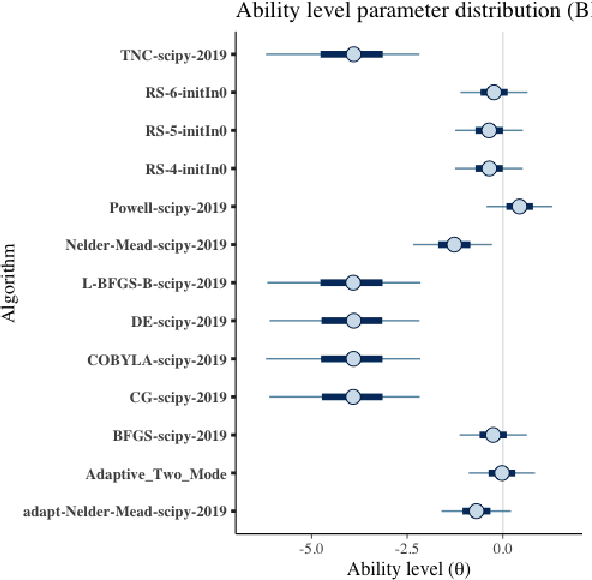
Benchmark suites, i.e. a collection of benchmark functions, are widely used in the comparison of black-box optimization algorithms. Over the years, research has identified many desired qualities for benchmark suites, such as diverse topology, different difficulties, scalability, representativeness of real-world problems among others. However, while the topology characteristics have been subjected to previous studies, there is no study that has statistically evaluated the difficulty level of benchmark functions, how well they discriminate optimization algorithms and how suitable is a benchmark suite for algorithm comparison. In this paper, we propose the use of an item response theory (IRT) model, the Bayesian two-parameter logistic model for multiple attempts, to statistically evaluate these aspects with respect to the empirical success rate of algorithms. With this model, we can assess the difficulty level of each benchmark, how well they discriminate different algorithms, the ability score of an algorithm, and how much information the benchmark suite adds in the estimation of the ability scores. We demonstrate the use of this model in two well-known benchmark suites, the Black-Box Optimization Benchmark (BBOB) for continuous optimization and the Pseudo Boolean Optimization (PBO) for discrete optimization. We found that most benchmark functions of BBOB suite have high difficulty levels (compared to the optimization algorithms) and low discrimination. For the PBO, most functions have good discrimination parameters but are often considered too easy. We discuss potential uses of IRT in benchmarking, including its use to improve the design of benchmark suites, to measure multiple aspects of the algorithms, and to design adaptive suites.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge