On State Variables, Bandit Problems and POMDPs
Paper and Code
Feb 14, 2020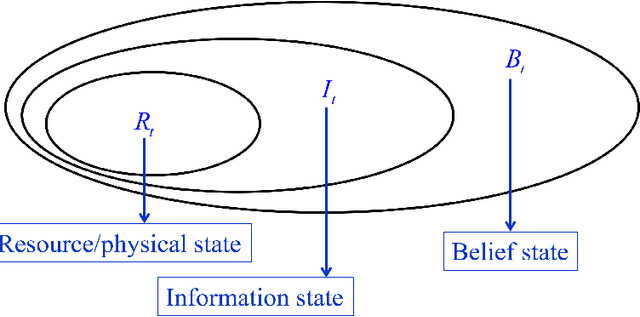


State variables are easily the most subtle dimension of sequential decision problems. This is especially true in the context of active learning problems (bandit problems") where decisions affect what we observe and learn. We describe our canonical framework that models {\it any} sequential decision problem, and present our definition of state variables that allows us to claim: Any properly modeled sequential decision problem is Markovian. We then present a novel two-agent perspective of partially observable Markov decision problems (POMDPs) that allows us to then claim: Any model of a real decision problem is (possibly) non-Markovian. We illustrate these perspectives using the context of observing and treating flu in a population, and provide examples of all four classes of policies in this setting. We close with an indication of how to extend this thinking to multiagent problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge