On Sex, Evolution, and the Multiplicative Weights Update Algorithm
Paper and Code
Feb 17, 2015
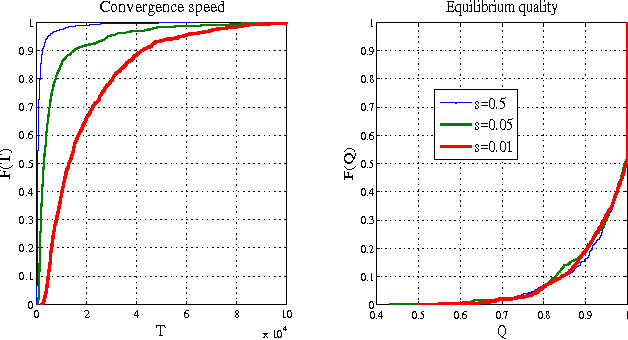

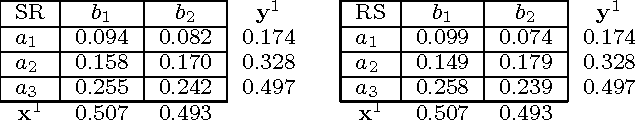
We consider a recent innovative theory by Chastain et al. on the role of sex in evolution [PNAS'14]. In short, the theory suggests that the evolutionary process of gene recombination implements the celebrated multiplicative weights updates algorithm (MWUA). They prove that the population dynamics induced by sexual reproduction can be precisely modeled by genes that use MWUA as their learning strategy in a particular coordination game. The result holds in the environments of \emph{weak selection}, under the assumption that the population frequencies remain a product distribution. We revisit the theory, eliminating both the requirement of weak selection and any assumption on the distribution of the population. Removing the assumption of product distributions is crucial, since as we show, this assumption is inconsistent with the population dynamics. We show that the marginal allele distributions induced by the population dynamics precisely match the marginals induced by a multiplicative weights update algorithm in this general setting, thereby affirming and substantially generalizing these earlier results. We further revise the implications for convergence and utility or fitness guarantees in coordination games. In contrast to the claim of Chastain et al.[PNAS'14], we conclude that the sexual evolutionary dynamics does not entail any property of the population distribution, beyond those already implied by convergence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge