On robust overfitting: adversarial training induced distribution matters
Paper and Code
Nov 28, 2023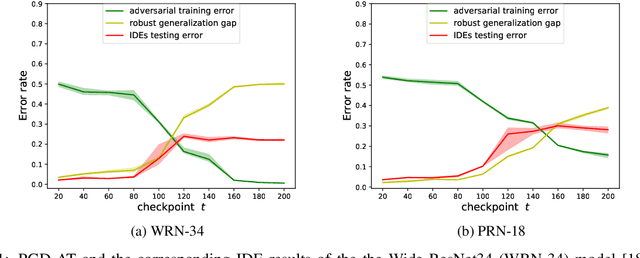

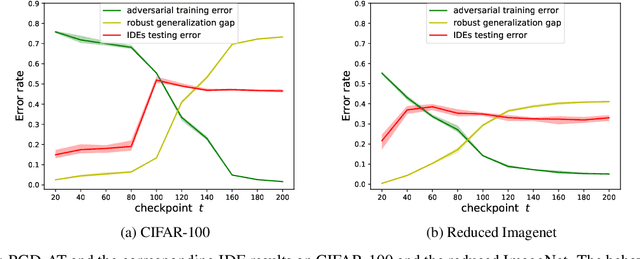
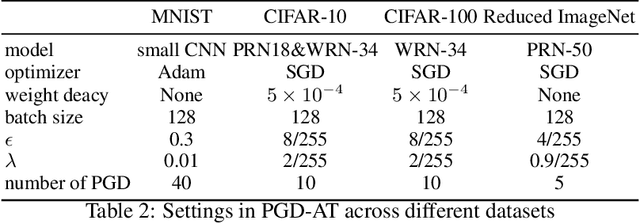
Adversarial training may be regarded as standard training with a modified loss function. But its generalization error appears much larger than standard training under standard loss. This phenomenon, known as robust overfitting, has attracted significant research attention and remains largely as a mystery. In this paper, we first show empirically that robust overfitting correlates with the increasing generalization difficulty of the perturbation-induced distributions along the trajectory of adversarial training (specifically PGD-based adversarial training). We then provide a novel upper bound for generalization error with respect to the perturbation-induced distributions, in which a notion of the perturbation operator, referred to "local dispersion", plays an important role.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge