On nondeterminism in combinatorial filters
Paper and Code
Jul 15, 2021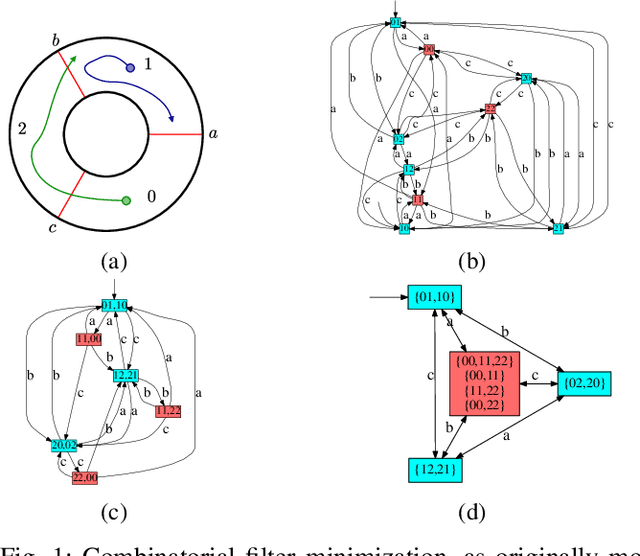
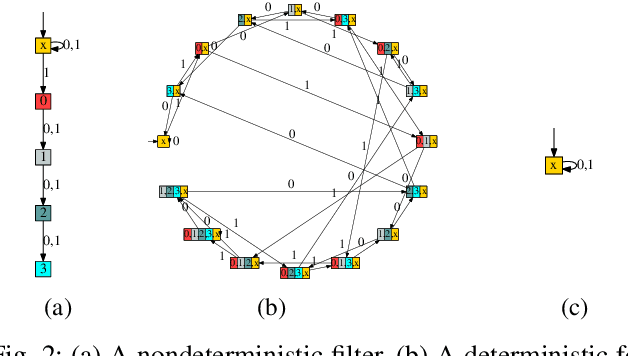
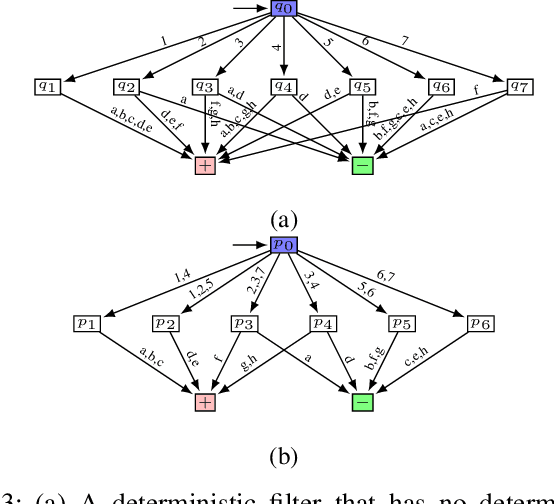
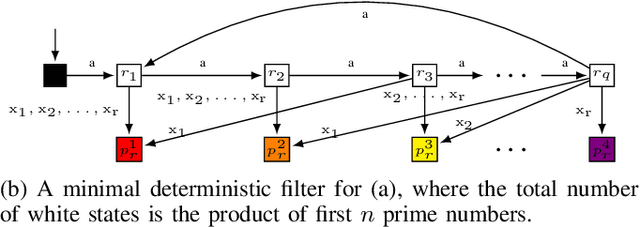
The problem of combinatorial filter reduction arises from questions of resource optimization in robots; it is one specific way in which automation can help to achieve minimalism, to build better, simpler robots. This paper contributes a new definition of filter minimization that is broader than its antecedents, allowing filters (input, output, or both) to be nondeterministic. This changes the problem considerably. Nondeterministic filters are able to re-use states to obtain, essentially, more 'behavior' per vertex. We show that the gap in size can be significant (larger than polynomial), suggesting such cases will generally be more challenging than deterministic problems. Indeed, this is supported by the core computational complexity result established in this paper: producing nondeterministic minimizers is PSPACE-hard. The hardness separation for minimization which exists between deterministic filter and deterministic automata, thus, does not hold for the nondeterministic case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge