On minimizers and convolutional filters: a partial justification for the unreasonable effectiveness of CNNs in categorical sequence analysis

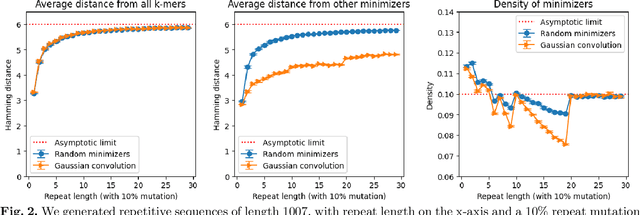
Minimizers and convolutional neural networks (CNNs) are two quite distinct popular techniques that have both been employed to analyze biological sequences. At face value, the methods seem entirely dissimilar. Minimizers use min-wise hashing on a rolling window to extract a single important k-mer feature per window. CNNs start with a wide array of randomly initialized convolutional filters, paired with a pooling operation, and then multiple additional neural layers to learn both the filters themselves and how those filters can be used to classify the sequence. In this manuscript, I demonstrate through a careful mathematical analysis of hash function properties that there are deep theoretical connections between minimizers and convolutional filters -- in short, for sequences over a categorical alphabet, random Gaussian initialization of convolutional filters with max-pooling is equivalent to choosing minimizers from a random hash function biased towards more distinct k-mers. This provides a partial explanation for the unreasonable effectiveness of CNNs in categorical sequence analysis.