On Loss Functions for Deep Neural Networks in Classification
Paper and Code
Feb 18, 2017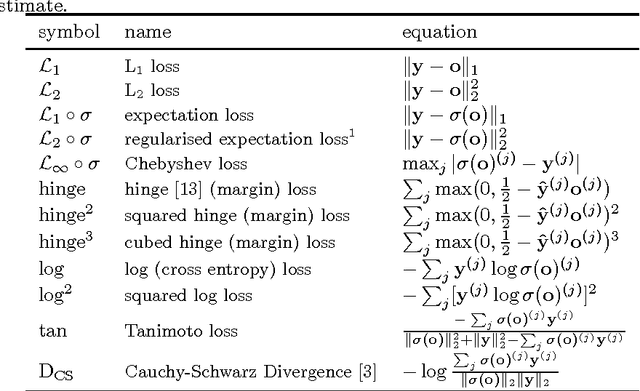
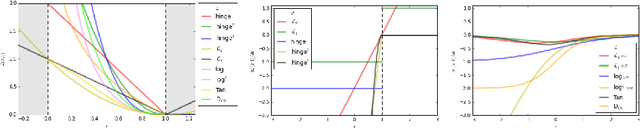
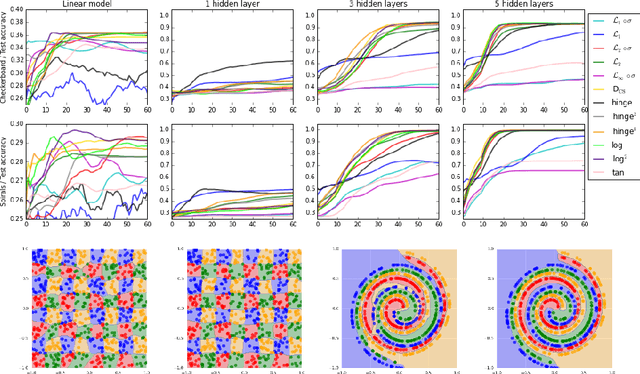
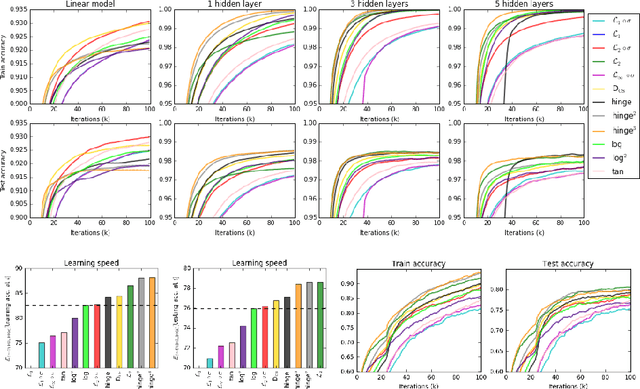
Deep neural networks are currently among the most commonly used classifiers. Despite easily achieving very good performance, one of the best selling points of these models is their modular design - one can conveniently adapt their architecture to specific needs, change connectivity patterns, attach specialised layers, experiment with a large amount of activation functions, normalisation schemes and many others. While one can find impressively wide spread of various configurations of almost every aspect of the deep nets, one element is, in authors' opinion, underrepresented - while solving classification problems, vast majority of papers and applications simply use log loss. In this paper we try to investigate how particular choices of loss functions affect deep models and their learning dynamics, as well as resulting classifiers robustness to various effects. We perform experiments on classical datasets, as well as provide some additional, theoretical insights into the problem. In particular we show that L1 and L2 losses are, quite surprisingly, justified classification objectives for deep nets, by providing probabilistic interpretation in terms of expected misclassification. We also introduce two losses which are not typically used as deep nets objectives and show that they are viable alternatives to the existing ones.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge