On Fast Johnson-Lindenstrauss Embeddings of Compact Submanifolds of $\mathbb{R}^N$ with Boundary
Paper and Code
Oct 28, 2021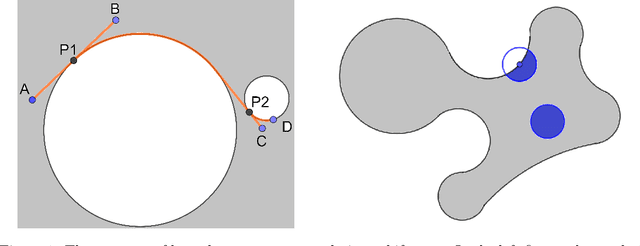
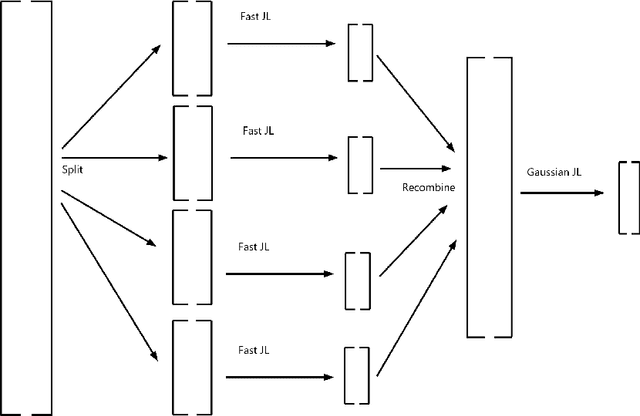
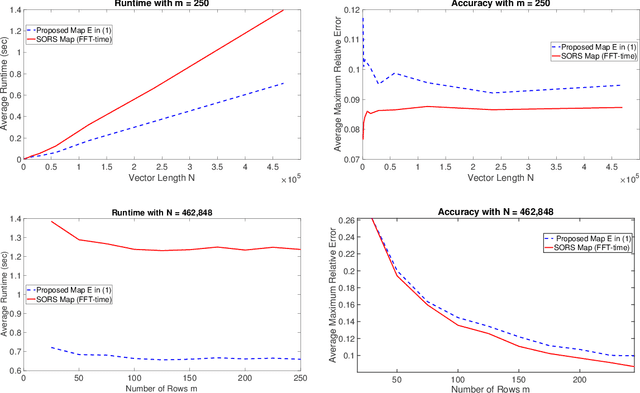
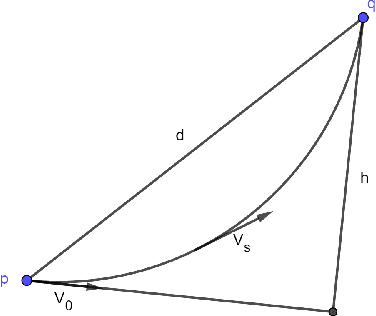
Let $\mathcal{M}$ be a smooth $d$-dimensional submanifold of $\mathbb{R}^N$ with boundary that's equipped with the Euclidean (chordal) metric, and choose $m \leq N$. In this paper we consider the probability that a random matrix $A \in \mathbb{R}^{m \times N}$ will serve as a bi-Lipschitz function $A: \mathcal{M} \rightarrow \mathbb{R}^m$ with bi-Lipschitz constants close to one for three different types of distributions on the $m \times N$ matrices $A$, including two whose realizations are guaranteed to have fast matrix-vector multiplies. In doing so we generalize prior randomized metric space embedding results of this type for submanifolds of $\mathbb{R}^N$ by allowing for the presence of boundary while also retaining, and in some cases improving, prior lower bounds on the achievable embedding dimensions $m$ for which one can expect small distortion with high probability. In particular, motivated by recent modewise embedding constructions for tensor data, herein we present a new class of highly structured distributions on matrices which outperform prior structured matrix distributions for embedding sufficiently low-dimensional submanifolds of $\mathbb{R}^N$ (with $d \lesssim \sqrt{N}$) with respect to both achievable embedding dimension, and computationally efficient realizations. As a consequence we are able to present, for example, a general new class of Johnson-Lindenstrauss embedding matrices for $\mathcal{O}(\log^c N)$-dimensional submanifolds of $\mathbb{R}^N$ which enjoy $\mathcal{O}(N \log (\log N))$-time matrix vector multiplications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge