On Constraint Definability in Tractable Probabilistic Models
Paper and Code
Jan 29, 2020
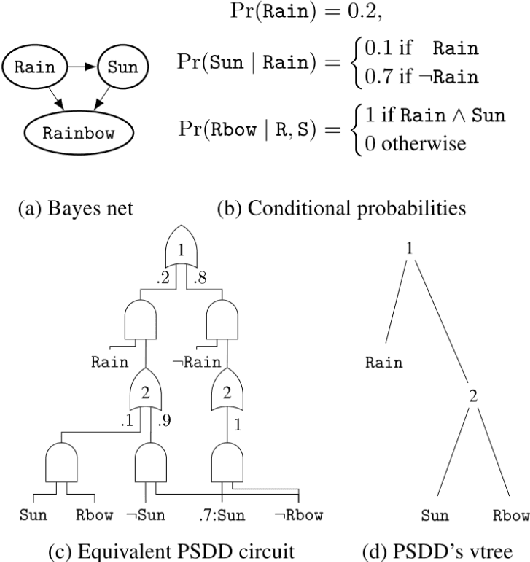
Incorporating constraints is a major concern in probabilistic machine learning. A wide variety of problems require predictions to be integrated with reasoning about constraints, from modelling routes on maps to approving loan predictions. In the former, we may require the prediction model to respect the presence of physical paths between the nodes on the map, and in the latter, we may require that the prediction model respect fairness constraints that ensure that outcomes are not subject to bias. Broadly speaking, constraints may be probabilistic, logical or causal, but the overarching challenge is to determine if and how a model can be learnt that handles all the declared constraints. To the best of our knowledge, this is largely an open problem. In this paper, we consider a mathematical inquiry on how the learning of tractable probabilistic models, such as sum-product networks, is possible while incorporating constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge