On consistent vertex nomination schemes

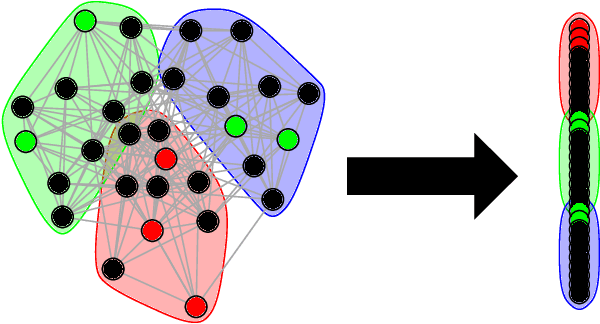
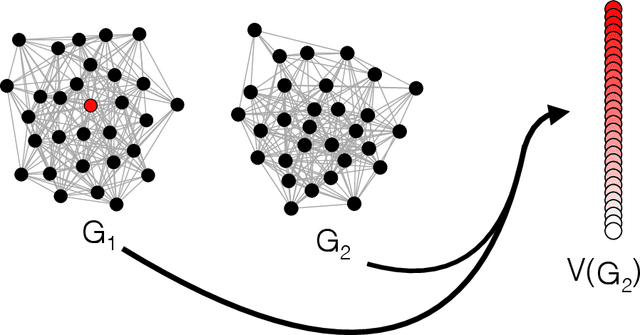
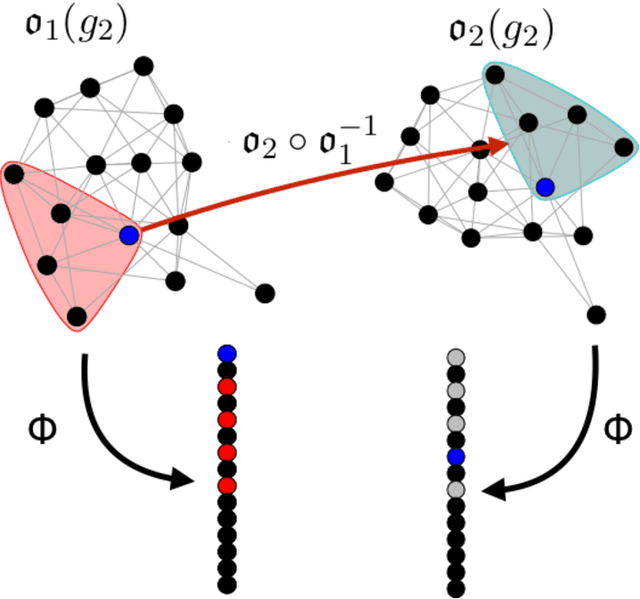
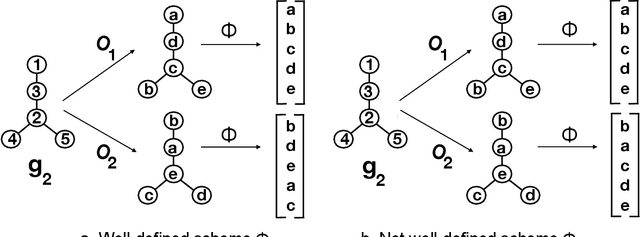
Given a vertex of interest in a network $G_1$, the vertex nomination problem seeks to find the corresponding vertex of interest (if it exists) in a second network $G_2$. A vertex nomination scheme produces a rank list of the vertices in $G_2$, where the vertices are ranked by how likely they are judged to be the corresponding vertex of interest in $G_2$. The vertex nomination problem and related information retrieval tasks have attracted much attention in the machine learning literature, with numerous applications in social and biological networks. However, the current framework has often been confined to a comparatively small class of network models, and the concept of statistically consistent vertex nomination schemes has been only shallowly explored. In this paper, we extend the vertex nomination problem to a very general statistical model of graphs. Further, drawing inspiration from the long-established classification framework in the pattern recognition literature, we provide definitions for the key notions of Bayes optimality and consistency in our extended vertex nomination framework, including a derivation of the Bayes optimal vertex nomination scheme. In addition, we prove that no universally consistent vertex nomination schemes exist. Illustrative examples are provided throughout.