On consistency of constrained spectral clustering under representation-aware stochastic block model
Paper and Code
Mar 03, 2022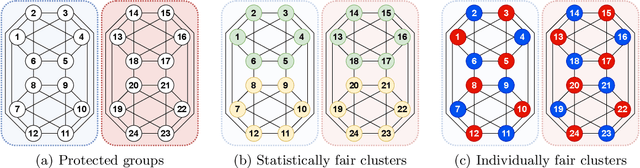
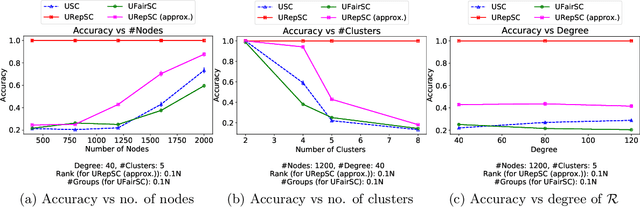
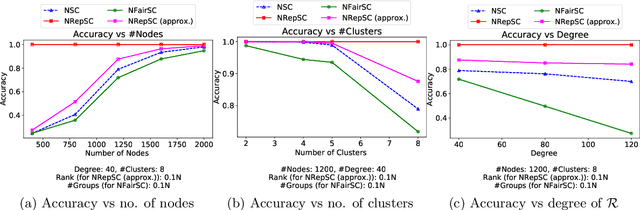
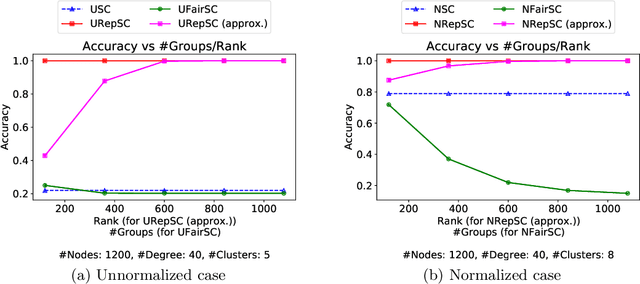
Spectral clustering is widely used in practice due to its flexibility, computational efficiency, and well-understood theoretical performance guarantees. Recently, spectral clustering has been studied to find balanced clusters under population-level constraints. These constraints are specified by additional information available in the form of auxiliary categorical node attributes. In this paper, we consider a scenario where these attributes may not be observable, but manifest as latent features of an auxiliary graph. Motivated by this, we study constrained spectral clustering with the aim of finding balanced clusters in a given \textit{similarity graph} $\mathcal{G}$, such that each individual is adequately represented with respect to an auxiliary graph $\mathcal{R}$ (we refer to this as representation graph). We propose an individual-level balancing constraint that formalizes this idea. Our work leads to an interesting stochastic block model that not only plants the given partitions in $\mathcal{G}$ but also plants the auxiliary information encoded in the representation graph $\mathcal{R}$. We develop unnormalized and normalized variants of spectral clustering in this setting. These algorithms use $\mathcal{R}$ to find clusters in $\mathcal{G}$ that approximately satisfy the proposed constraint. We also establish the first statistical consistency result for constrained spectral clustering under individual-level constraints for graphs sampled from the above-mentioned variant of the stochastic block model. Our experimental results corroborate our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge