On Certifying Non-uniform Bound against Adversarial Attacks
Paper and Code
Mar 15, 2019
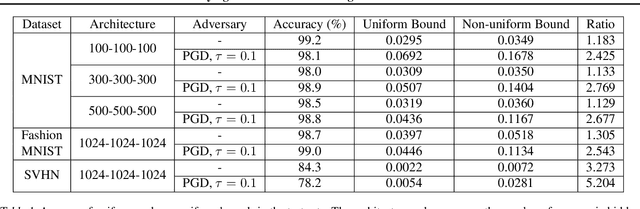
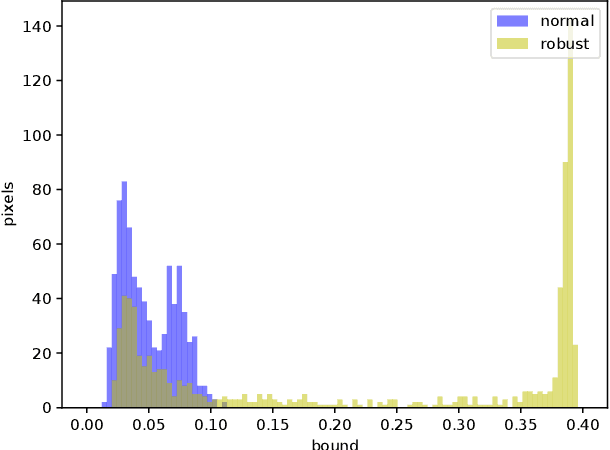
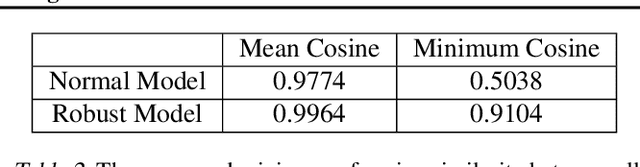
This work studies the robustness certification problem of neural network models, which aims to find certified adversary-free regions as large as possible around data points. In contrast to the existing approaches that seek regions bounded uniformly along all input features, we consider non-uniform bounds and use it to study the decision boundary of neural network models. We formulate our target as an optimization problem with nonlinear constraints. Then, a framework applicable for general feedforward neural networks is proposed to bound the output logits so that the relaxed problem can be solved by the augmented Lagrangian method. Our experiments show the non-uniform bounds have larger volumes than uniform ones. Compared with normal models, the robust models have even larger non-uniform bounds and better interpretability. Further, the geometric similarity of the non-uniform bounds gives a quantitative, data-agnostic metric of input features' robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge