Offline Task Assistance Planning on a Graph:Theoretic and Algorithmic Foundations
Paper and Code
Sep 10, 2024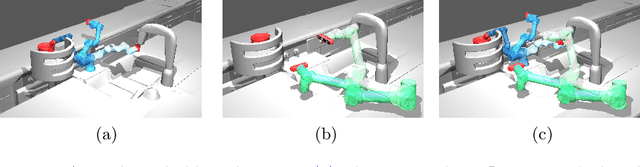

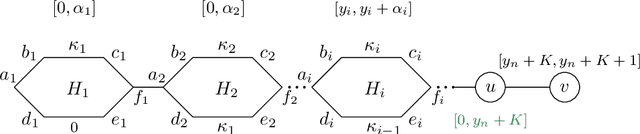
In this work we introduce the problem of task assistance planning where we are given two robots Rtask and Rassist. The first robot, Rtask, is in charge of performing a given task by executing a precomputed path. The second robot, Rassist, is in charge of assisting the task performed by Rtask using on-board sensors. The ability of Rassist to provide assistance to Rtask depends on the locations of both robots. Since Rtask is moving along its path, Rassist may also need to move to provide as much assistance as possible. The problem we study is how to compute a path for Rassist so as to maximize the portion of Rtask's path for which assistance is provided. We limit the problem to the setting where Rassist moves on a roadmap which is a graph embedded in its configuration space and show that this problem is NP-hard. Fortunately, we show that when Rassist moves on a given path, and all we have to do is compute the times at which Rassist should move from one configuration to the following one, we can solve the problem optimally in polynomial time. Together with carefully-crafted upper bounds, this polynomial-time algorithm is integrated into a Branch and Bound-based algorithm that can compute optimal solutions to the problem outperforming baselines by several orders of magnitude. We demonstrate our work empirically in simulated scenarios containing both planar manipulators and UR robots as well as in the lab on real robots.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge