O$^2$TD: -Optimal Off-Policy TD Learning

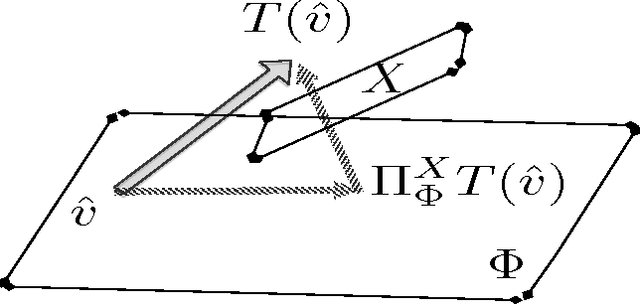
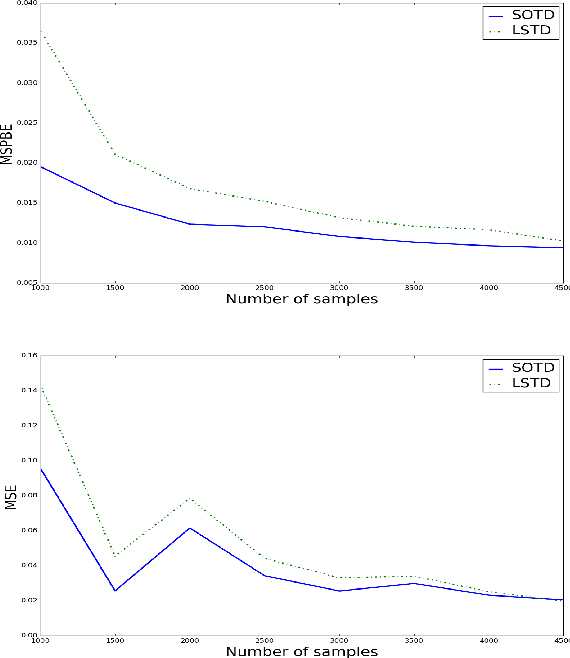
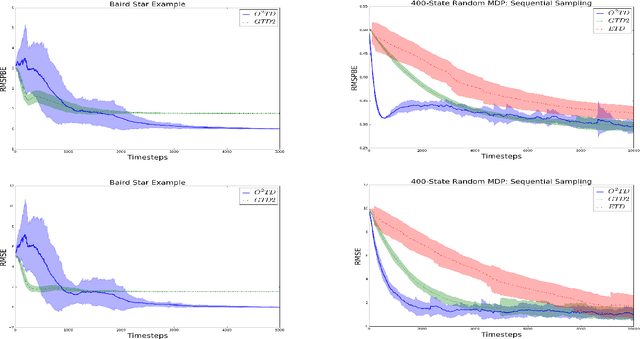
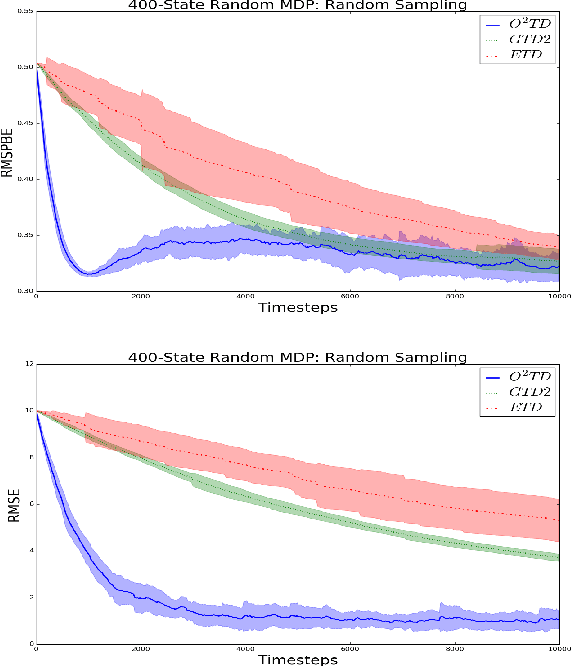
Temporal difference learning and Residual Gradient methods are the most widely used temporal difference based learning algorithms; however, it has been shown that none of their objective functions is optimal w.r.t approximating the true value function $V$. Two novel algorithms are proposed to approximate the true value function $V$. This paper makes the following contributions: (1) A batch algorithm that can help find the approximate optimal off-policy prediction of the true value function $V$. (2) A linear computational cost (per step) near-optimal algorithm that can learn from a collection of off-policy samples. (3) A new perspective of the emphatic temporal difference learning which bridges the gap between off-policy optimality and off-policy stability.