Nyström Approximation with Nonnegative Matrix Factorization

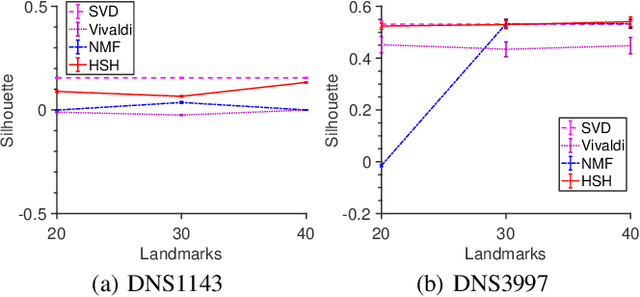
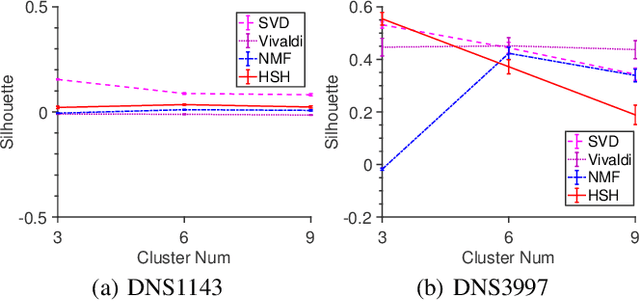
Motivated by the needs of estimating the proximity clustering with partial distance measurements from vantage points or landmarks for remote networked systems, we show that the proximity clustering problem can be effectively formulated as the Nystr\"om approximation problem, which solves the kernel K-means clustering problem in the complex space. We implement the Nystr\"om approximation based on a landmark based Nonnegative Matrix Factorization (NMF) process. Evaluation results show that the proposed method finds nearly optimal clustering quality on both synthetic and real-world data sets as we vary the range of parameter choices and network conditions.