Nonuniform Sampling Rate Conversion: An Efficient Approach
Paper and Code
May 14, 2021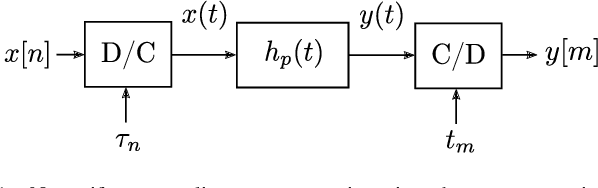



We present a discrete-time algorithm for nonuniform sampling rate conversion that presents low computational complexity and memory requirements. It generalizes arbitrary sampling rate conversion by accommodating time-varying conversion ratios, i.e., it can efficiently adapt to instantaneous changes of the input and output sampling rates. This approach is based on appropriately factorizing the time-varying discrete-time filter used for the conversion. Common filters that satisfy this factorization property are those where the underlying continuous-time filter consists of linear combinations of exponentials, e.g., those described by linear constant-coefficient differential equations. This factorization separates the computation into two parts: one consisting of a factor solely depending on the output sampling instants and the other consists of a summation -- that can be computed recursively -- whose terms depend solely on the input sampling instants and its number of terms is given by a relationship between input and output sampling instants. Thus, nonuniform sampling rates can be accommodated by updating the factors involved and adjusting the number of terms added. When the impulse response consists of exponentials, computing the factors can be done recursively in an efficient manner.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge