Nondeterminism subject to output commitment in combinatorial filters
Paper and Code
Apr 01, 2022
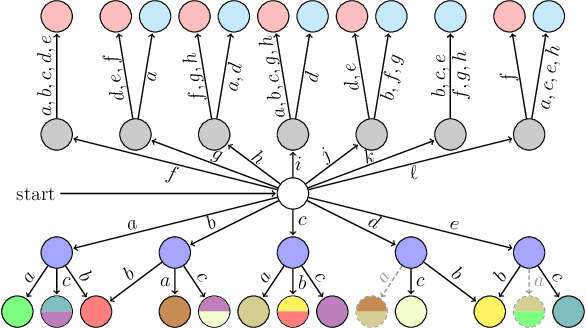
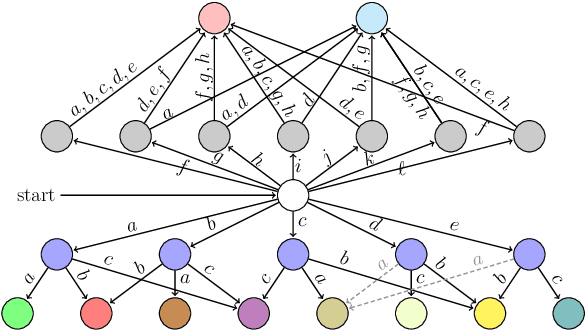
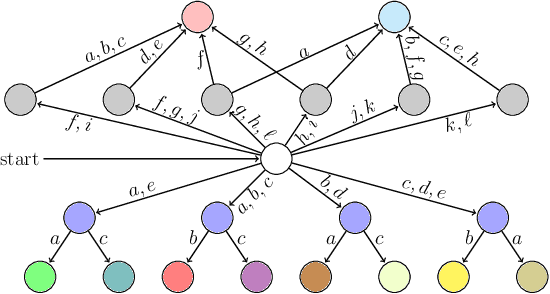
We study a class of filters -- discrete finite-state transition systems employed as incremental stream transducers -- that have application to robotics: e.g., to model combinatorial estimators and also as concise encodings of feedback plans/policies. The present paper examines their minimization problem under some new assumptions. Compared to strictly deterministic filters, allowing nondeterminism supplies opportunities for compression via re-use of states. But this paper suggests that the classic automata-theoretic concept of nondeterminism, though it affords said opportunities for reduction in state complexity, is problematic in many robotics settings. Instead, we argue for a new constrained type of nondeterminism that preserves input-output behavior for circumstances when, as for robots, causation forbids 'rewinding' of the world. We identify problem instances where compression under this constrained form of nondeterminism results in improvements over all deterministic filters. In this new setting, we examine computational complexity questions for the problem of reducing the state complexity of some given input filter. A hardness result for general deterministic input filters is presented, as well as for checking specific, narrower requirements, and some special cases. These results show that this class of nondeterminism gives problems of the same complexity class as classical nondeterminism, and the narrower questions help give a more nuanced understanding of the source of this complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge