Nonasymptotic performance analysis of ESPRIT and spatial-smoothing ESPRIT
Paper and Code
Jan 10, 2022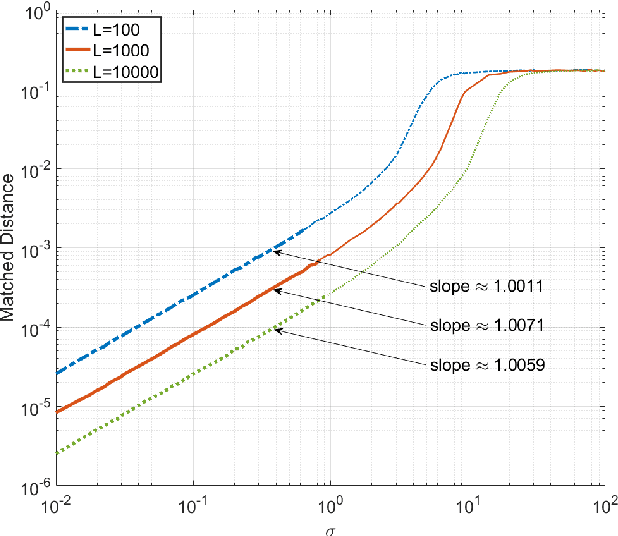
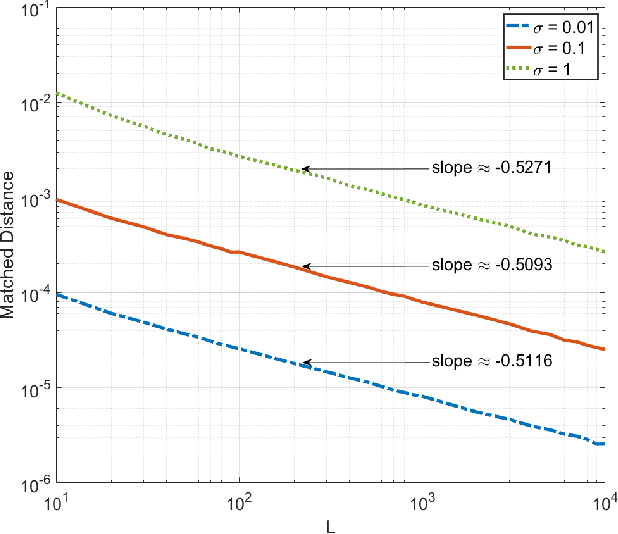
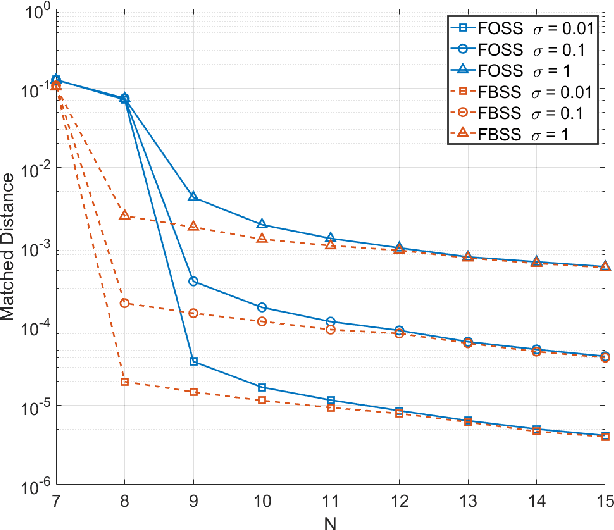
This paper is concerned with the problem of frequency estimation from multiple-snapshot data. It is well-known that ESPRIT (and spatial-smoothing ESPRIT in presence of coherent sources or given limited snapshots) can locate the true frequencies if either the number of snapshots or the signal-to-noise ratio (SNR) approaches infinity. In this paper, we analyze the nonasymptotic performance of ESPRIT and spatial-smoothing ESPRIT with finitely many snapshots and finite SNR. We show that the absolute frequency estimation error of ESPRIT (or spatial-smoothing ESPRIT) is bounded from above by $C\frac{\max(\sigma, \sigma^2)}{\sqrt{L}}$ with overwhelming probability, where $\sigma^2$ denotes the Gaussian noise variance, $L$ is the number of snapshots and $C$ is a coefficient independent of $L$ and $\sigma^2$, if and only if the true frequencies can be localized by ESPRIT (or spatial-smoothing ESPRIT) without noise or with infinitely many snapshots. Our results are obtained by deriving new matrix perturbation bounds and generalizing the classical Schur product theorem, which may be of independent interest. Extensions to MUSIC and SS-MUSIC are also made. Numerical results are provided corroborating our analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge