Non-linear Attributed Graph Clustering by Symmetric NMF with PU Learning
Paper and Code
Sep 21, 2018

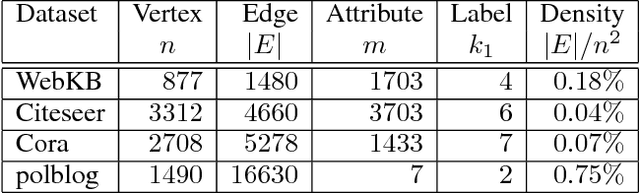

We consider the clustering problem of attributed graphs. Our challenge is how we can design an effective and efficient clustering method that precisely captures the hidden relationship between the topology and the attributes in real-world graphs. We propose Non-linear Attributed Graph Clustering by Symmetric Non-negative Matrix Factorization with Positive Unlabeled Learning. The features of our method are three holds. 1) it learns a non-linear projection function between the different cluster assignments of the topology and the attributes of graphs so as to capture the complicated relationship between the topology and the attributes in real-world graphs, 2) it leverages the positive unlabeled learning to take the effect of partially observed positive edges into the cluster assignment, and 3) it achieves efficient computational complexity, $O((n^2+mn)kt)$, where $n$ is the vertex size, $m$ is the attribute size, $k$ is the number of clusters, and $t$ is the number of iterations for learning the cluster assignment. We conducted experiments extensively for various clustering methods with various real datasets to validate that our method outperforms the former clustering methods regarding the clustering quality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge