Non-Gaussian information from weak lensing data via deep learning
Paper and Code
May 01, 2018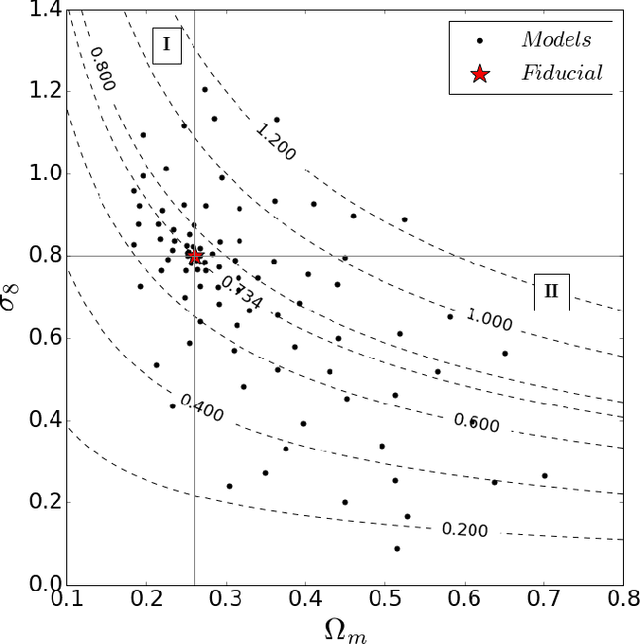
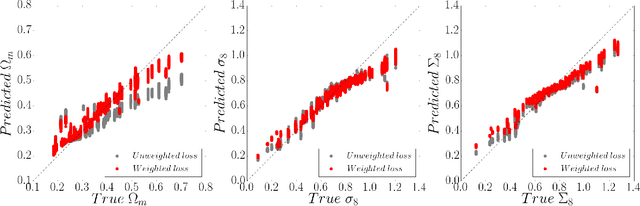
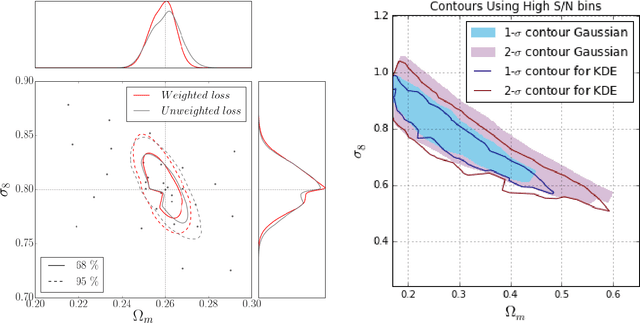
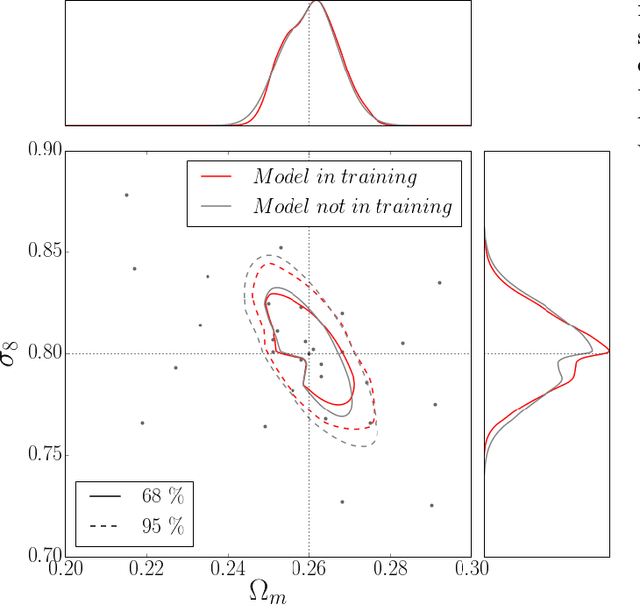
Weak lensing maps contain information beyond two-point statistics on small scales. Much recent work has tried to extract this information through a range of different observables or via nonlinear transformations of the lensing field. Here we train and apply a 2D convolutional neural network to simulated noiseless lensing maps covering 96 different cosmological models over a range of {$\Omega_m,\sigma_8$}. Using the area of the confidence contour in the {$\Omega_m,\sigma_8$} plane as a figure-of-merit, derived from simulated convergence maps smoothed on a scale of 1.0 arcmin, we show that the neural network yields $\approx 5 \times$ tighter constraints than the power spectrum, and $\approx 4 \times$ tighter than the lensing peaks. Such gains illustrate the extent to which weak lensing data encode cosmological information not accessible to the power spectrum or even other, non-Gaussian statistics such as lensing peaks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge