Newton-Type Iterative Solver for Multiple View $L2$ Triangulation
Paper and Code
Jun 30, 2014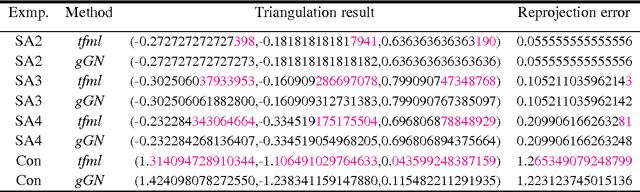
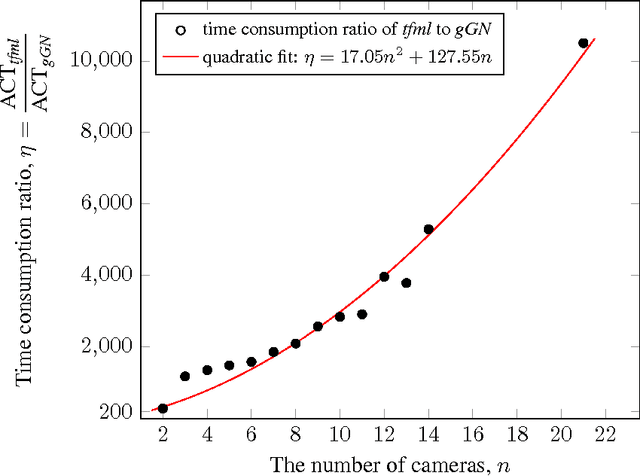
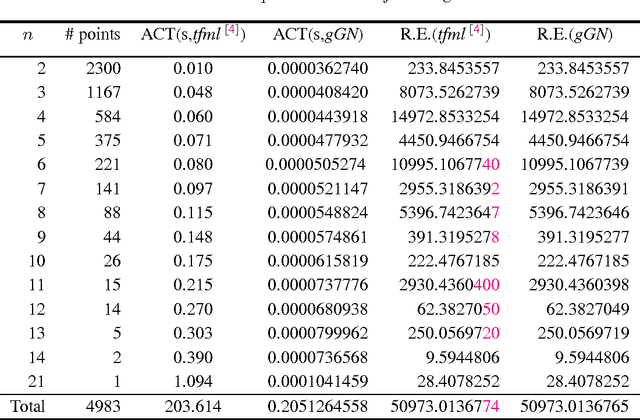
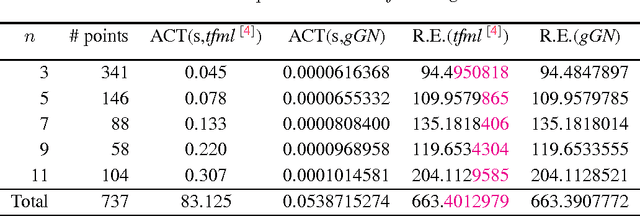
In this note, we show that the L2 optimal solutions to most real multiple view L2 triangulation problems can be efficiently obtained by two-stage Newton-like iterative methods, while the difficulty of such problems mainly lies in how to verify the L2 optimality. Such a working two-stage bundle adjustment approach features: first, the algorithm is initialized by symmedian point triangulation, a multiple-view generalization of the mid-point method; second, a symbolic-numeric method is employed to compute derivatives accurately; third, globalizing strategy such as line search or trust region is smoothly applied to the underlying iteration which assures algorithm robustness in general cases. Numerical comparison with tfml method shows that the local minimizers obtained by the two-stage iterative bundle adjustment approach proposed here are also the L2 optimal solutions to all the calibrated data sets available online by the Oxford visual geometry group. Extensive numerical experiments indicate the bundle adjustment approach solves more than 99% the real triangulation problems optimally. An IEEE 754 double precision C++ implementation shows that it takes only about 0.205 second tocompute allthe 4983 points in the Oxford dinosaur data setvia Gauss-Newton iteration hybrid with a line search strategy on a computer with a 3.4GHz Intel i7 CPU.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge