New Advances in Inference by Recursive Conditioning
Paper and Code
Oct 19, 2012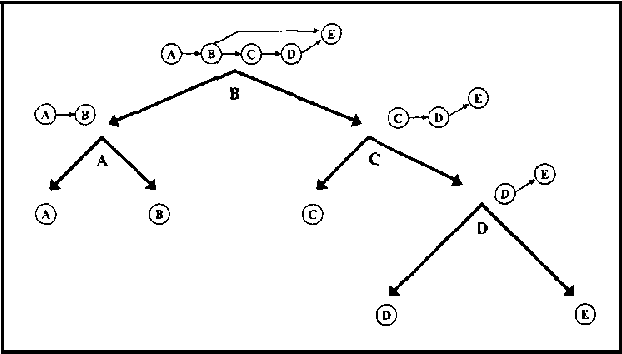
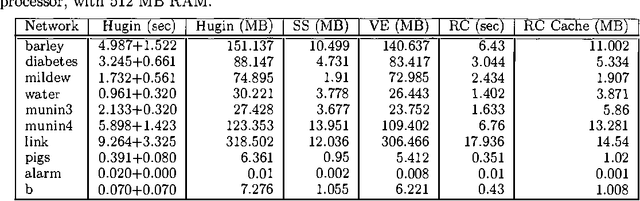
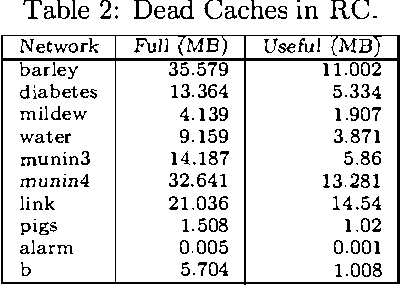
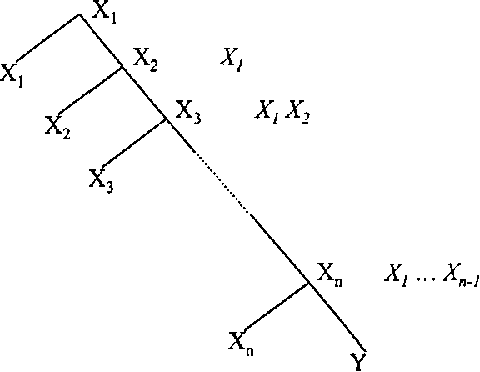
Recursive Conditioning (RC) was introduced recently as the first any-space algorithm for inference in Bayesian networks which can trade time for space by varying the size of its cache at the increment needed to store a floating point number. Under full caching, RC has an asymptotic time and space complexity which is comparable to mainstream algorithms based on variable elimination and clustering (exponential in the network treewidth and linear in its size). We show two main results about RC in this paper. First, we show that its actual space requirements under full caching are much more modest than those needed by mainstream methods and study the implications of this finding. Second, we show that RC can effectively deal with determinism in Bayesian networks by employing standard logical techniques, such as unit resolution, allowing a significant reduction in its time requirements in certain cases. We illustrate our results using a number of benchmark networks, including the very challenging ones that arise in genetic linkage analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge