Neural network wave functions and the sign problem
Paper and Code
Feb 21, 2020
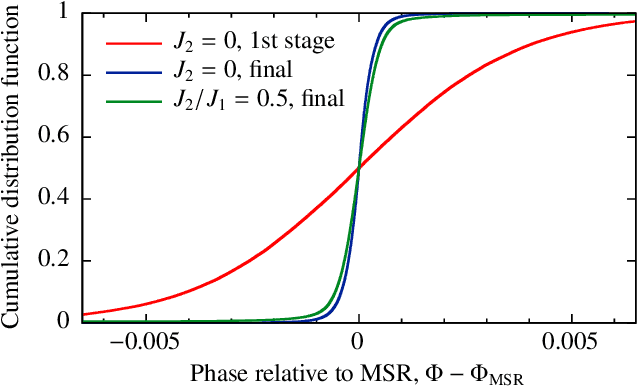


Neural quantum states (NQS) are a promising approach to study many-body quantum physics. However, they face a major challenge when applied to lattice models: Convolutional networks struggle to converge to ground states with a nontrivial sign structure. We tackle this problem by proposing a neural network architecture with a simple, explicit, and interpretable phase ansatz, which can robustly represent such states and achieve state-of-the-art variational energies for both conventional and frustrated antiferromagnets. In the latter case, our approach uncovers low-energy states that exhibit the Marshall sign rule and are therefore inconsistent with the expected ground state. Such states are the likely cause of the obstruction for NQS-based variational Monte Carlo to access the true ground states of these systems. We discuss the implications of this observation and suggest potential strategies to overcome the problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge