Neural Network based on Automatic Differentiation Transformation of Numeric Iterate-to-Fixedpoint

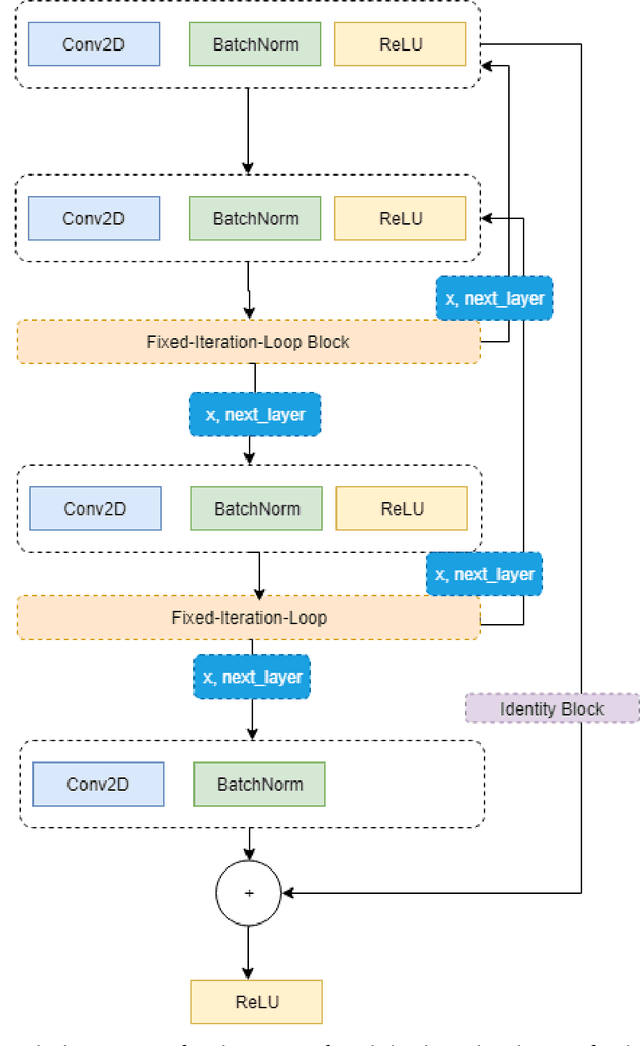
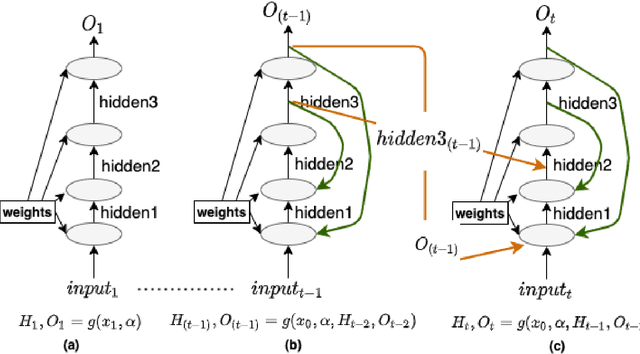
This work proposes a Neural Network model that can control its depth using an iterate-to-fixed-point operator. The architecture starts with a standard layered Network but with added connections from current later to earlier layers, along with a gate to make them inactive under most circumstances. These ``temporal wormhole'' connections create a shortcut that allows the Neural Network to use the information available at deeper layers and re-do earlier computations with modulated inputs. End-to-end training is accomplished by using appropriate calculations for a numeric iterate-to-fixed-point operator. In a typical case, where the ``wormhole'' connections are inactive, this is inexpensive; but when they are active, the network takes a longer time to settle down, and the gradient calculation is also more laborious, with an effect similar to making the network deeper. In contrast to the existing skip-connection concept, this proposed technique enables information to flow up and down in the network. Furthermore, the flow of information follows a fashion that seems analogous to the afferent and efferent flow of information through layers of processing in the brain. We evaluate models that use this novel mechanism on different long-term dependency tasks. The results are competitive with other studies, showing that the proposed model contributes significantly to overcoming traditional deep learning models' vanishing gradient descent problem. At the same time, the training time is significantly reduced, as the ``easy'' input cases are processed more quickly than ``difficult'' ones.