Network driven sampling; a critical threshold for design effects
Paper and Code
Jun 01, 2017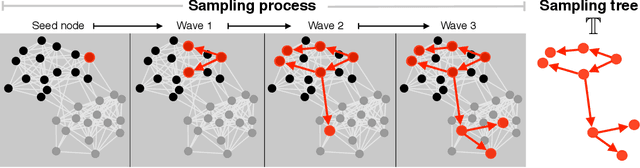
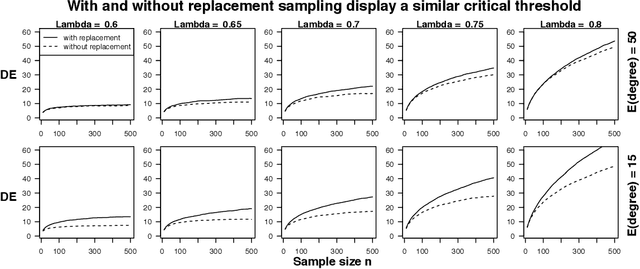
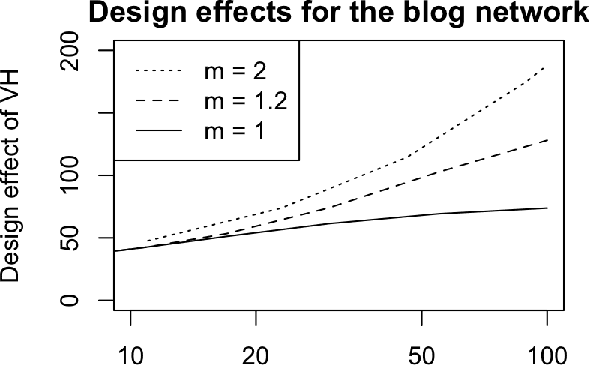
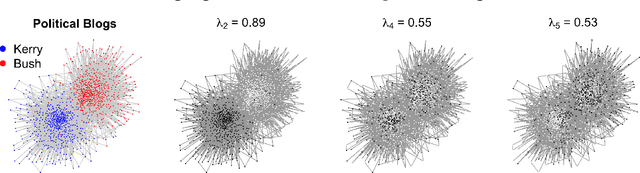
Web crawling, snowball sampling, and respondent-driven sampling (RDS) are three types of network sampling techniques used to contact individuals in hard-to-reach populations. This paper studies these procedures as a Markov process on the social network that is indexed by a tree. Each node in this tree corresponds to an observation and each edge in the tree corresponds to a referral. Indexing with a tree (instead of a chain) allows for the sampled units to refer multiple future units into the sample. In survey sampling, the design effect characterizes the additional variance induced by a novel sampling strategy. If the design effect is some value $DE$, then constructing an estimator from the novel design makes the variance of the estimator $DE$ times greater than it would be under a simple random sample with the same sample size $n$. Under certain assumptions on the referral tree, the design effect of network sampling has a critical threshold that is a function of the referral rate $m$ and the clustering structure in the social network, represented by the second eigenvalue of the Markov transition matrix, $\lambda_2$. If $m < 1/\lambda_2^2$, then the design effect is finite (i.e. the standard estimator is $\sqrt{n}$-consistent). However, if $m > 1/\lambda_2^2$, then the design effect grows with $n$ (i.e. the standard estimator is no longer $\sqrt{n}$-consistent). Past this critical threshold, the standard error of the estimator converges at the slower rate of $n^{\log_m \lambda_2}$. The Markov model allows for nodes to be resampled; computational results show that the findings hold in without-replacement sampling. To estimate confidence intervals that adapt to the correct level of uncertainty, a novel resampling procedure is proposed. Computational experiments compare this procedure to previous techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge