neos: End-to-End-Optimised Summary Statistics for High Energy Physics
Paper and Code
Mar 10, 2022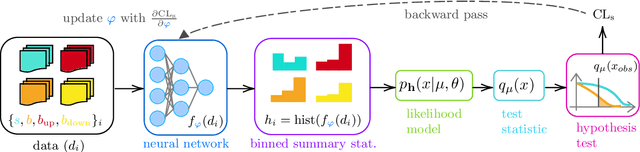
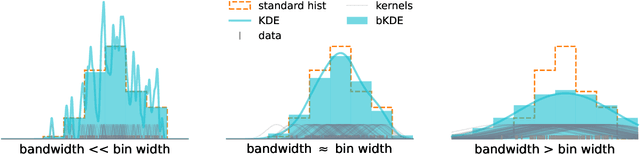
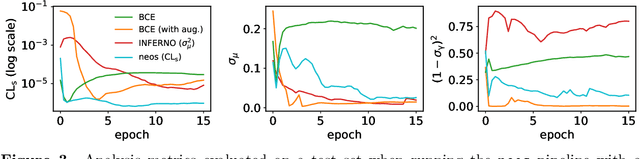
The advent of deep learning has yielded powerful tools to automatically compute gradients of computations. This is because training a neural network equates to iteratively updating its parameters using gradient descent to find the minimum of a loss function. Deep learning is then a subset of a broader paradigm; a workflow with free parameters that is end-to-end optimisable, provided one can keep track of the gradients all the way through. This work introduces neos: an example implementation following this paradigm of a fully differentiable high-energy physics workflow, capable of optimising a learnable summary statistic with respect to the expected sensitivity of an analysis. Doing this results in an optimisation process that is aware of the modelling and treatment of systematic uncertainties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge