Nearly Tight Convergence Bounds for Semi-discrete Entropic Optimal Transport
Paper and Code
Oct 25, 2021
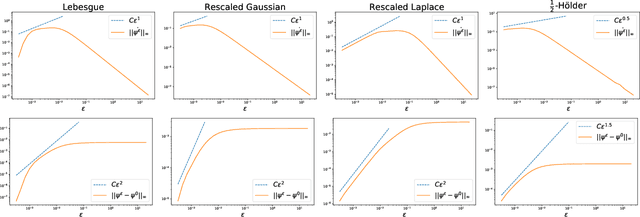
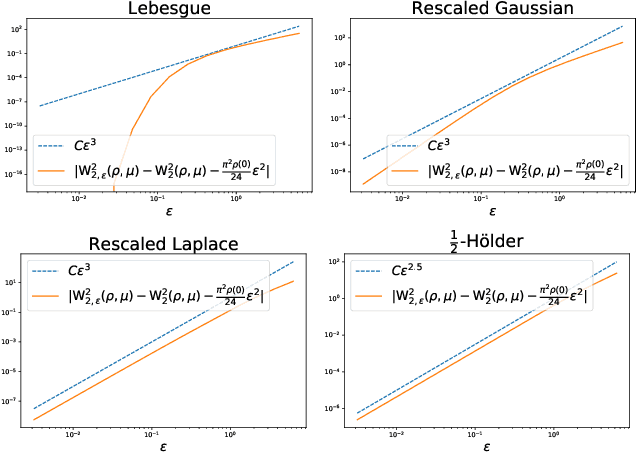
We derive nearly tight and non-asymptotic convergence bounds for solutions of entropic semi-discrete optimal transport. These bounds quantify the stability of the dual solutions of the regularized problem (sometimes called Sinkhorn potentials) w.r.t. the regularization parameter, for which we ensure a better than Lipschitz dependence. Such facts may be a first step towards a mathematical justification of annealing or $\eps$-scaling heuristics for the numerical resolution of regularized semi-discrete optimal transport. Our results also entail a non-asymptotic and tight expansion of the difference between the entropic and the unregularized costs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge