Nearest Empirical Distribution: An Asymptotically Optimal Algorithm For Supervised Classification of Data Vectors with Independent Non-Identically Distributed Elements

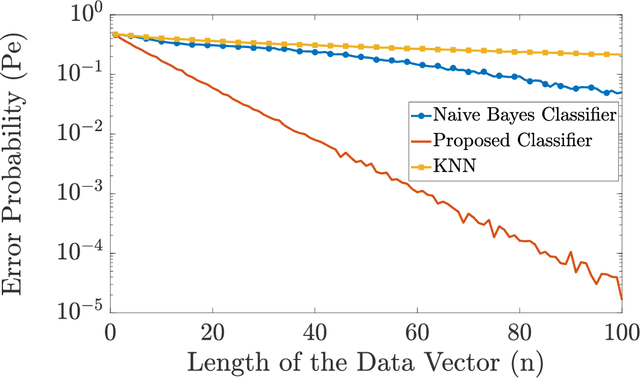
In this paper, we propose a classifier for supervised classification of data vectors with mutually independent but non-identically distributed elements. For the proposed classifier, we derive an upper bound on the error probability and show that the error probability goes to zero as the length of the data vectors grows, even when there is only one training data vector per label available. As a result, the proposed classifier is asymptomatically optimal for this type of data vectors. Our numerical examples show that the performance of the proposed classifier outperforms conventional classification algorithms when the number of training data is small and the length of the data vectors is sufficiently high.