Near-Optimal Performance Bounds for Orthogonal and Permutation Group Synchronization via Spectral Methods

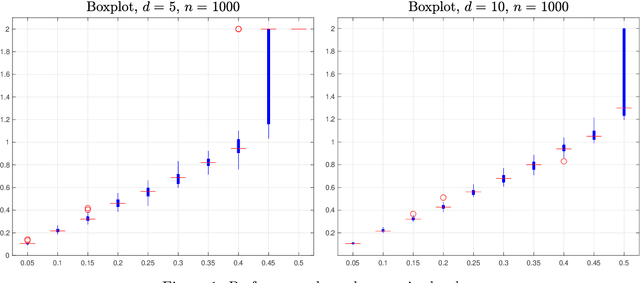
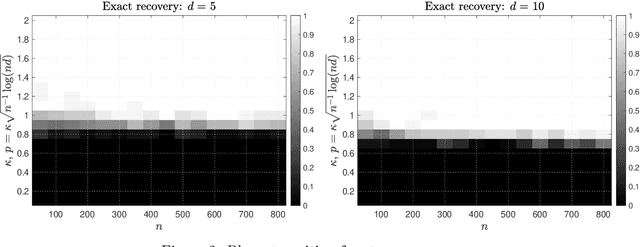
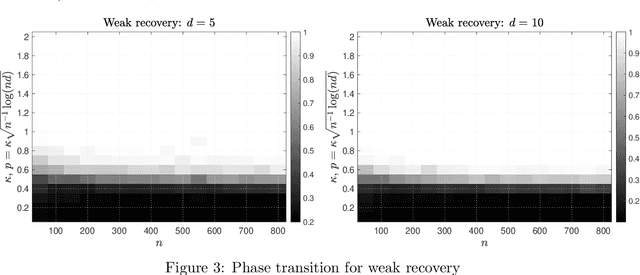
Group synchronization asks to recover group elements from their pairwise measurements. It has found numerous applications across various scientific disciplines. In this work, we focus on orthogonal and permutation group synchronization which are widely used in computer vision such as object matching and Structure from Motion. Among many available approaches, spectral methods have enjoyed great popularity due to its efficiency and convenience. We will study the performance guarantees of spectral methods in solving these two synchronization problems by investigating how well the computed eigenvectors approximate each group element individually. We establish our theory by applying the recent popular~\emph{leave-one-out} technique and derive a~\emph{block-wise} performance bound for the recovery of each group element via eigenvectors. In particular, for orthogonal group synchronization, we obtain a near-optimal performance bound for the group recovery in presence of Gaussian noise. For permutation group synchronization under random corruption, we show that the widely-used two-step procedure (spectral method plus rounding) can recover all the group elements exactly if the SNR (signal-to-noise ratio) is close to the information theoretical limit. Our numerical experiments confirm our theory and indicate a sharp phase transition for the exact group recovery.