Natural evolutionary strategies applied to quantum-classical hybrid neural networks

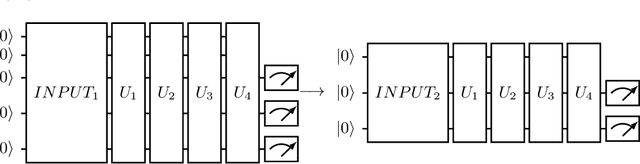
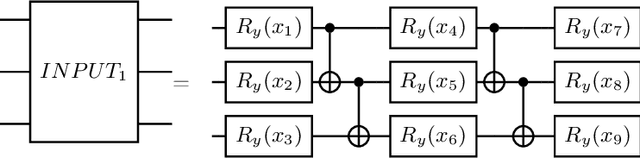
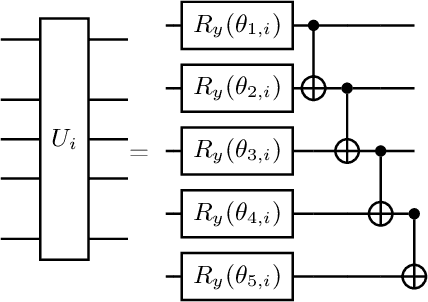
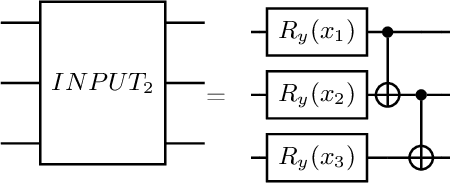
With the rapid development of quantum computers, several applications are being proposed for them. Quantum simulations, simulation of chemical reactions, solution of optimization problems and quantum neural networks are some examples. However, problems such as noise, limited number of qubits and circuit depth, and gradient vanishing must be resolved before we can use them to their full potential. In the field of quantum machine learning, several models have been proposed. In general, in order to train these different models, we use the gradient of a cost function with respect to the model parameters. In order to obtain this gradient, we must compute the derivative of this function with respect to the model parameters. For this we can use the method called parameter-shift rule. This method consists of evaluating the cost function twice for each parameter of the quantum network. A problem with this method is that the number of evaluations grows linearly with the number of parameters. In this work we study an alternative method, called Natural Evolutionary Strategies (NES), which are a family of black box optimization algorithms. An advantage of the NES method is that in using it one can control the number of times the cost function will be evaluated. We apply the NES method to the binary classification task, showing that this method is a viable alternative for training quantum neural networks.