Naming Games in Spatially-Embedded Random Networks

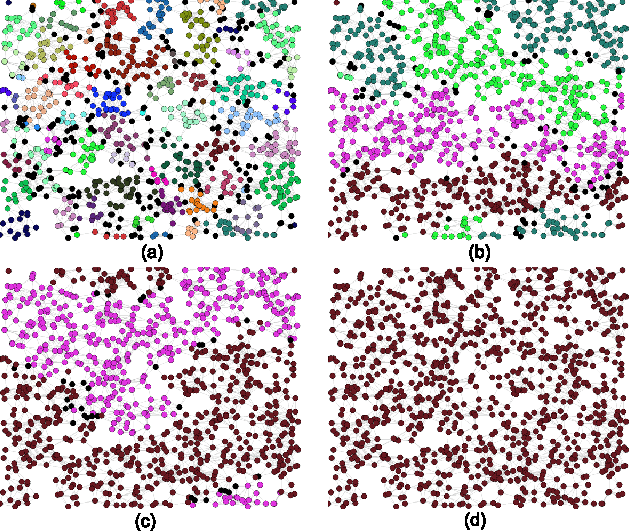
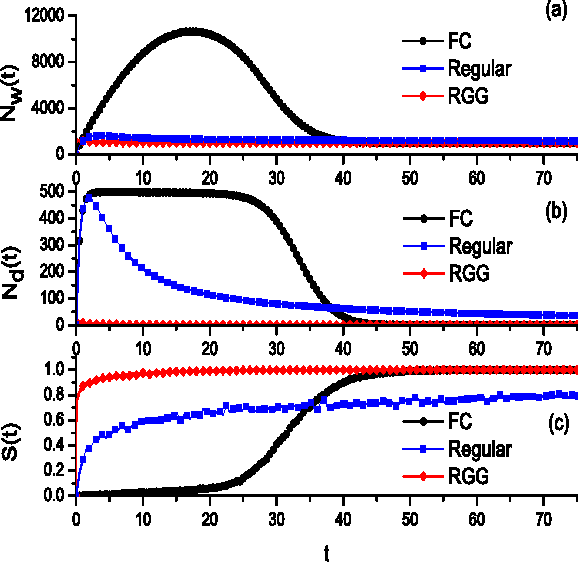
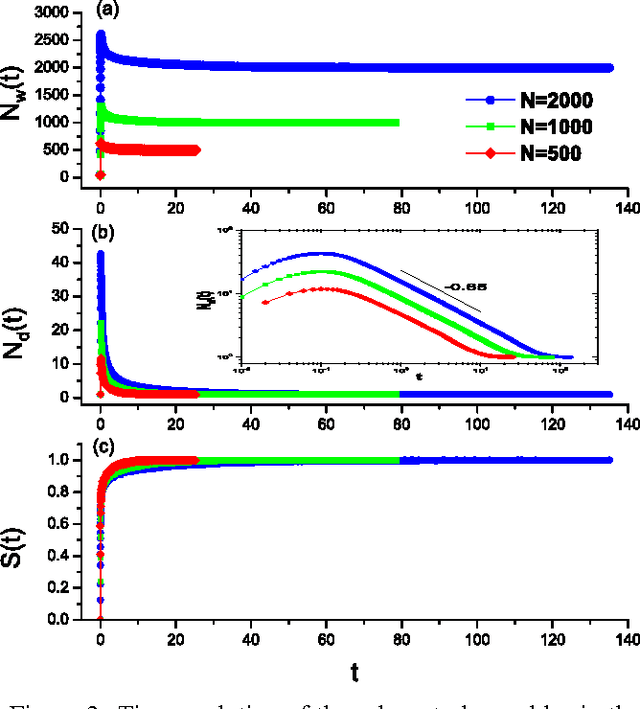
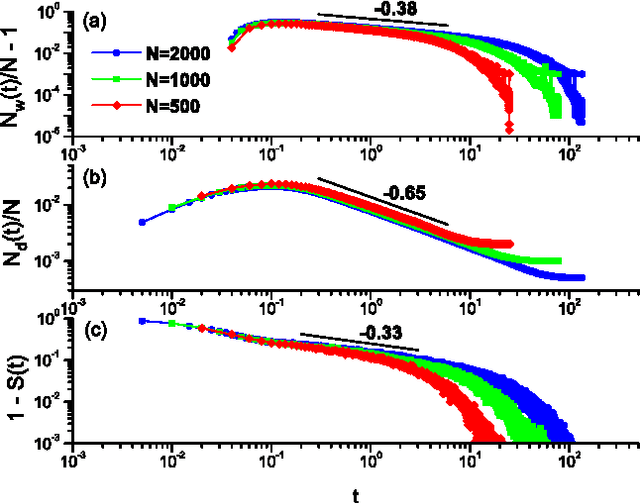
We investigate a prototypical agent-based model, the Naming Game, on random geometric networks. The Naming Game is a minimal model, employing local communications that captures the emergence of shared communication schemes (languages) in a population of autonomous semiotic agents. Implementing the Naming Games on random geometric graphs, local communications being local broadcasts, serves as a model for agreement dynamics in large-scale, autonomously operating wireless sensor networks. Further, it captures essential features of the scaling properties of the agreement process for spatially-embedded autonomous agents. We also present results for the case when a small density of long-range communication links are added on top of the random geometric graph, resulting in a "small-world"-like network and yielding a significantly reduced time to reach global agreement.