N-sphere chord length distribution
Paper and Code
Nov 20, 2014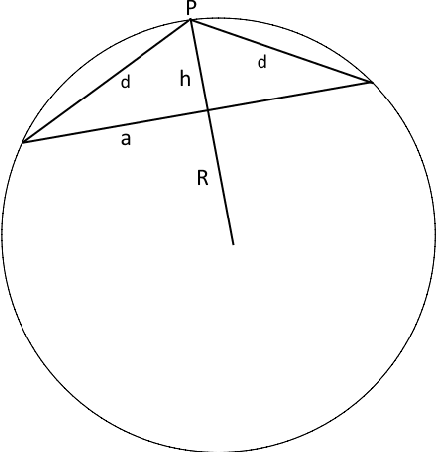


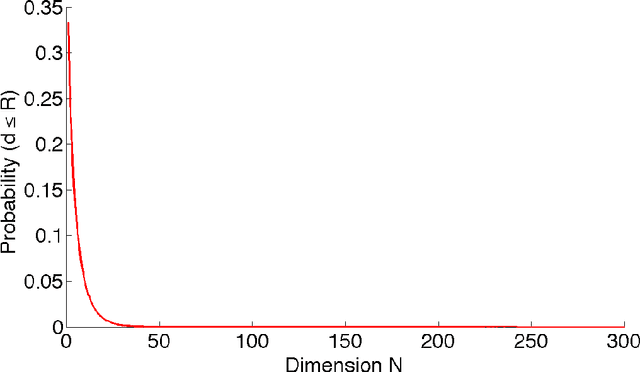
This work studies the chord length distribution, in the case where both ends lie on a $N$-dimensional hypersphere ($N \geq 2$). Actually, after connecting this distribution to the recently estimated surface of a hyperspherical cap \cite{SLi11}, closed-form expressions of both the probability density function and the cumulative distribution function are straightforwardly extracted, which are followed by a discussion on its basic properties, among which its dependence from the hypersphere dimension. Additionally, the distribution of the dot product of unitary vectors is estimated, a problem that is related to the chord length.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge