Multidimensional Interpolants

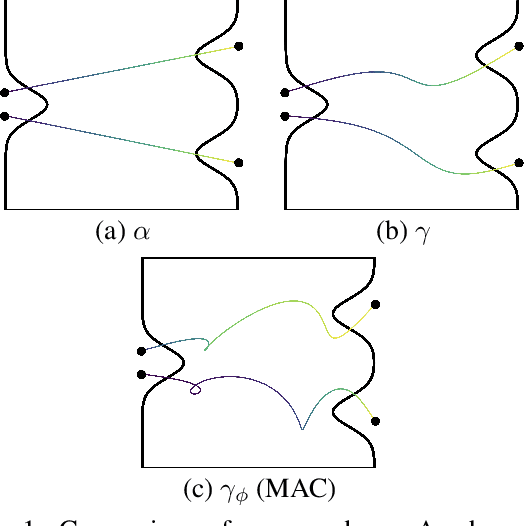
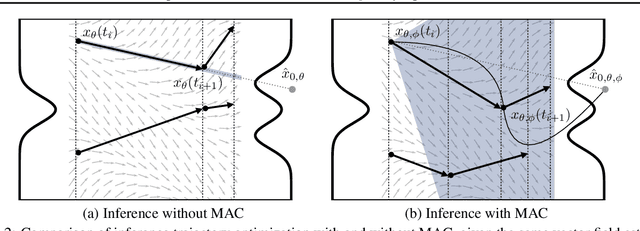
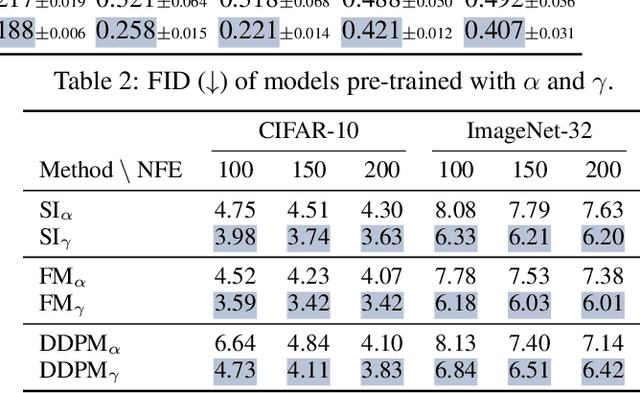
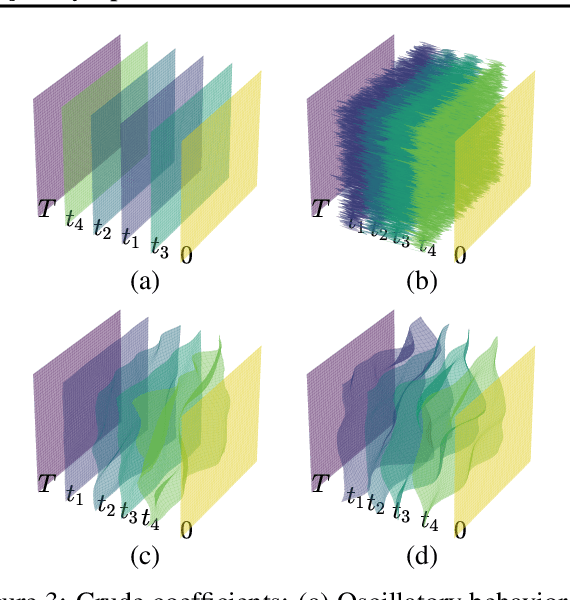
In the domain of differential equation-based generative modeling, conventional approaches often rely on single-dimensional scalar values as interpolation coefficients during both training and inference phases. In this work, we introduce, for the first time, a multidimensional interpolant that extends these coefficients into multiple dimensions, leveraging the stochastic interpolant framework. Additionally, we propose a novel path optimization problem tailored to adaptively determine multidimensional inference trajectories, with a predetermined differential equation solver and a fixed number of function evaluations. Our solution involves simulation dynamics coupled with adversarial training to optimize the inference path. Notably, employing a multidimensional interpolant during training improves the model's inference performance, even in the absence of path optimization. When the adaptive, multidimensional path derived from our optimization process is employed, it yields further performance gains, even with fixed solver configurations. The introduction of multidimensional interpolants not only enhances the efficacy of models but also opens up a new domain for exploration in training and inference methodologies, emphasizing the potential of multidimensional paths as an untapped frontier.