Multi-sensor Suboptimal Fusion Student's $t$ Filter
Paper and Code
Apr 23, 2022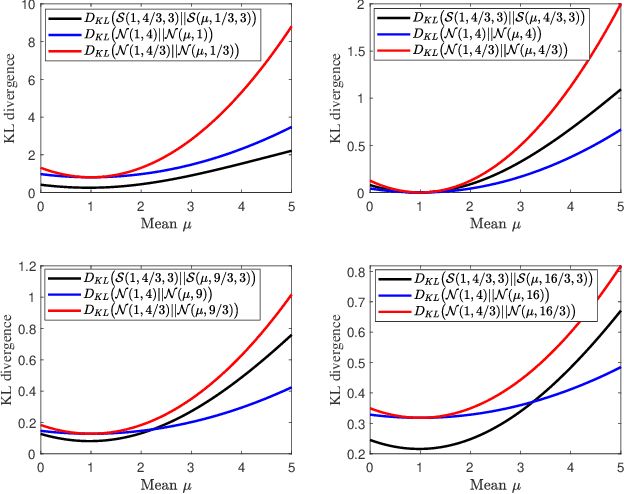
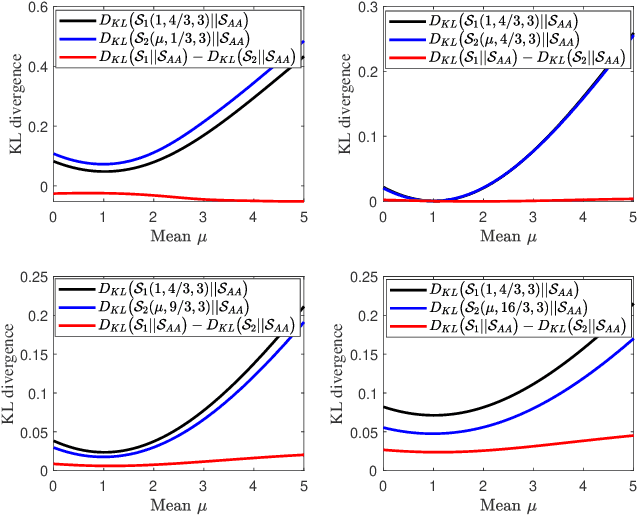
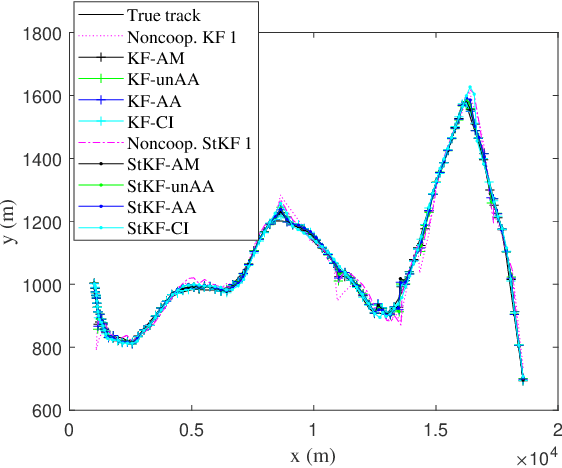
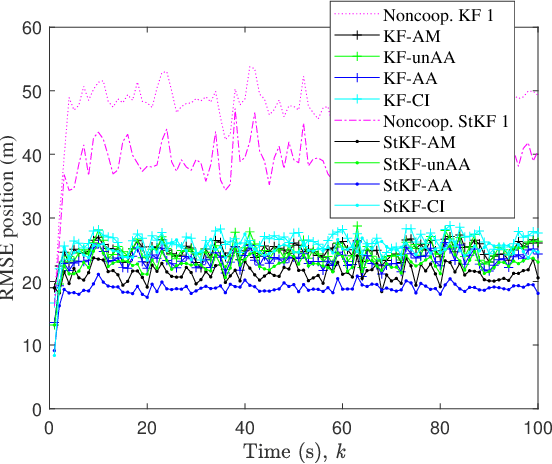
A multi-sensor fusion Student's $t$ filter is proposed for time-series recursive estimation in the presence of heavy-tailed process and measurement noises. Driven from an information-theoretic optimization, the approach extends the single sensor Student's $t$ Kalman filter based on the suboptimal arithmetic average (AA) fusion approach. To ensure computationally efficient, closed-form $t$ density recursion, reasonable approximation has been used in both local-sensor filtering and inter-sensor fusion calculation. The overall framework accommodates any Gaussian-oriented fusion approach such as the covariance intersection (CI). Simulation demonstrates the effectiveness of the proposed multi-sensor AA fusion-based $t$ filter in dealing with outliers as compared with the classic Gaussian estimator, and the advantage of the AA fusion in comparison with the CI approach and the augmented measurement fusion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge