Multi-mode Core Tensor Factorization based Low-Rankness and Its Applications to Tensor Completion

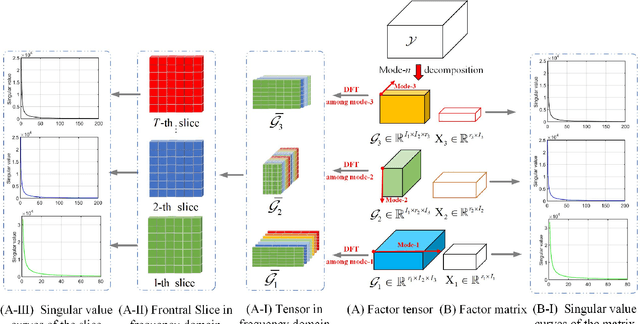
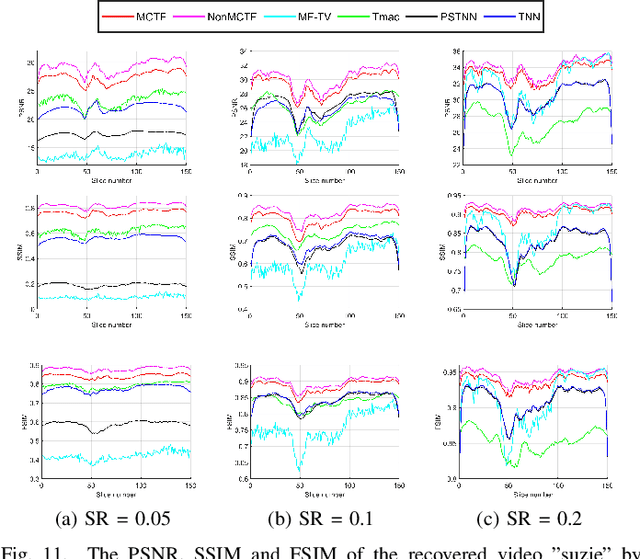
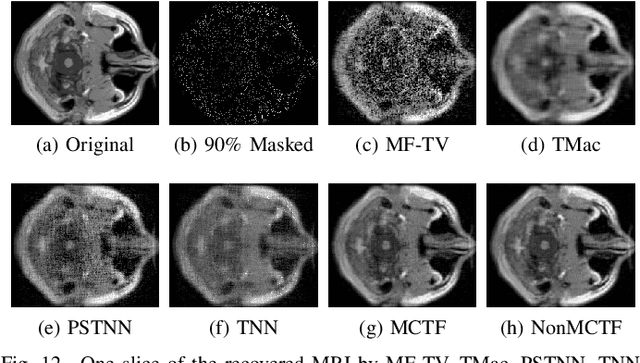
Low-rank tensor completion has been widely used in computer vision and machine learning. This paper develops a tensor low-rank decomposition method together with a tensor low-rankness measure (MCTF) and a better nonconvex relaxation form of it (NonMCTF). This is the first method that can accurately restore the clean data of intrinsic low-rank structure based on few known inputs. This metric encodes low-rank insights for general tensors provided by Tucker and T-SVD. Furthermore, we studied the MCTF and NonMCTF regularization minimization problem, and designed an effective BSUM algorithm to solve the problem. This efficient solver can extend MCTF to various tasks, such as tensor completion and tensor robust principal component analysis. A series of experiments, including hyperspectral image (HSI) denoising, video completion and MRI restoration, confirmed the superior performance of the proposed method