Multi-Kernel Diffusion CNNs for Graph-Based Learning on Point Clouds
Paper and Code
Sep 14, 2018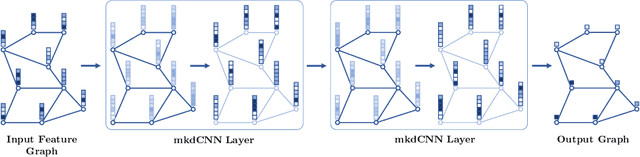



Graph convolutional networks are a new promising learning approach to deal with data on irregular domains. They are predestined to overcome certain limitations of conventional grid-based architectures and will enable efficient handling of point clouds or related graphical data representations, e.g. superpixel graphs. Learning feature extractors and classifiers on 3D point clouds is still an underdeveloped area and has potential restrictions to equal graph topologies. In this work, we derive a new architectural design that combines rotationally and topologically invariant graph diffusion operators and node-wise feature learning through 1x1 convolutions. By combining multiple isotropic diffusion operations based on the Laplace-Beltrami operator, we can learn an optimal linear combination of diffusion kernels for effective feature propagation across nodes on an irregular graph. We validated our approach for learning point descriptors as well as semantic classification on real 3D point clouds of human poses and demonstrate an improvement from 85% to 95% in Dice overlap with our multi-kernel approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge