Multi-Goal Multi-Agent Path Finding via Decoupled and Integrated Goal Vertex Ordering
Paper and Code
Sep 10, 2020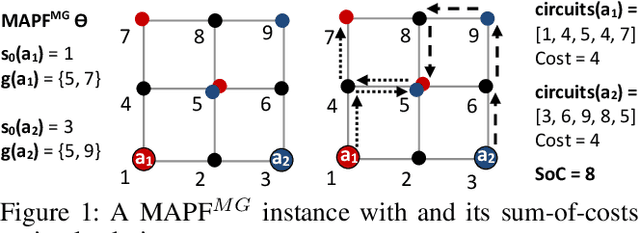
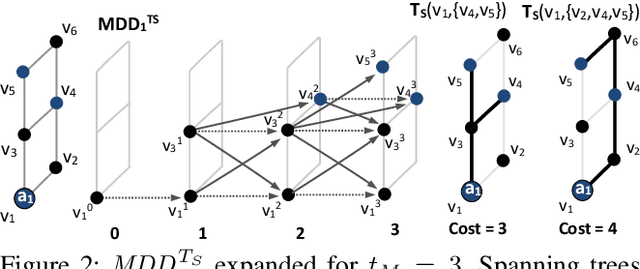
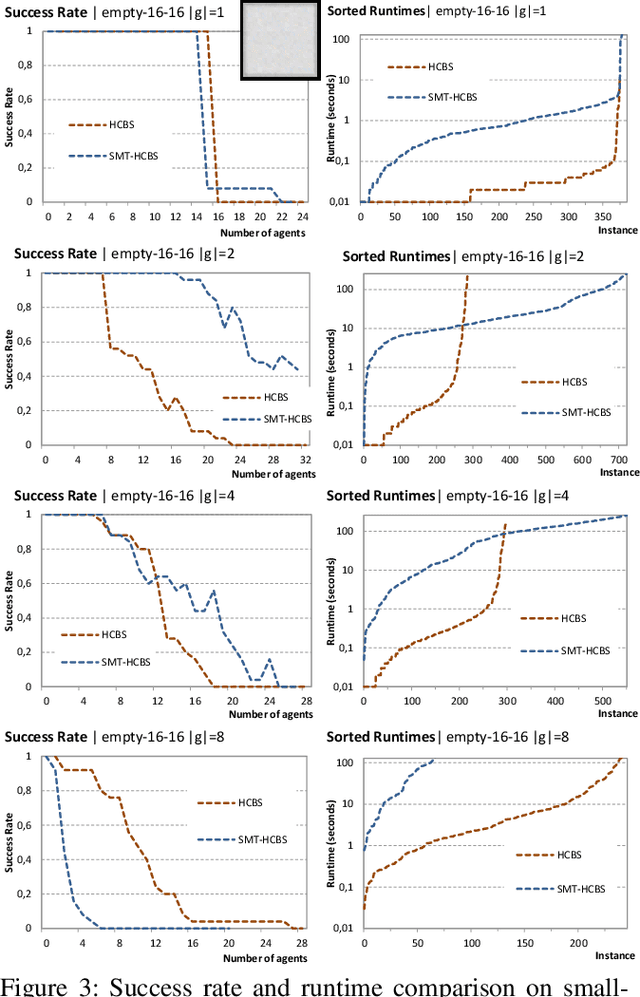
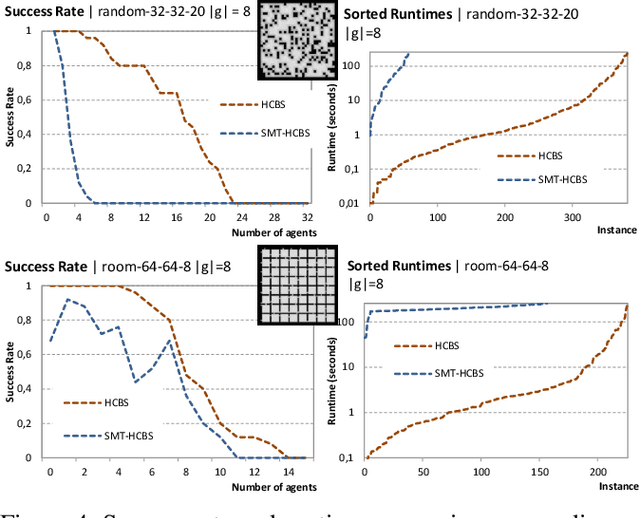
We introduce multi-goal multi agent path finding (MAPF$^{MG}$) which generalizes the standard discrete multi-agent path finding (MAPF) problem. While the task in MAPF is to navigate agents in an undirected graph from their starting vertices to one individual goal vertex per agent, MAPF$^{MG}$ assigns each agent multiple goal vertices and the task is to visit each of them at least once. Solving MAPF$^{MG}$ not only requires finding collision free paths for individual agents but also determining the order of visiting agent's goal vertices so that common objectives like the sum-of-costs are optimized. We suggest two novel algorithms using different paradigms to address MAPF$^{MG}$: a heuristic search-based search algorithm called Hamiltonian-CBS (HCBS) and a compilation-based algorithm built using the SMT paradigm, called SMT-Hamiltonian-CBS (SMT-HCBS). Experimental comparison suggests limitations of compilation-based approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge