Multi-dimensional Lorenz-Based Chaotic Waveforms for Wireless Power Transfer
Paper and Code
Oct 04, 2021
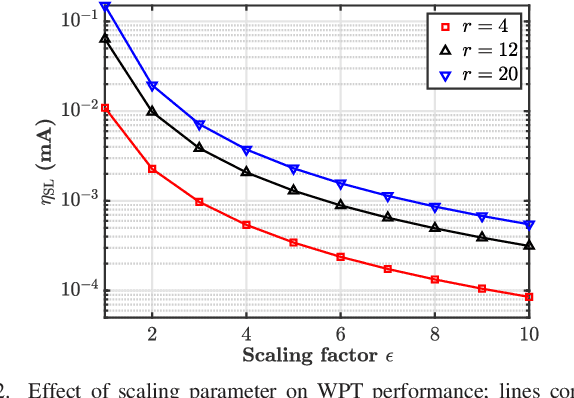


In this paper, we investigate multi-dimensional chaotic signals with respect to wireless power transfer (WPT). Specifically, we analyze a multi-dimensional Lorenz-based chaotic signal under a WPT framework. By taking into account the nonlinearities of the energy harvesting process, closed-form analytical expressions for the average harvested energy are derived. Moreover, the practical limitations of the high power amplifier (HPA) at the transmitter are also taken into consideration. We interestingly observe that for these types of signals, high peak-to-average-power-ratio (PAPR) is not the only criterion for obtaining enhanced WPT. We demonstrate that while the HPA imperfections do not significantly affect the signal PAPR, it notably degrades the energy transfer performance. As the proposed framework is general, we also demonstrate its application with respect to a Henon signal based WPT. Finally we compare Lorenz and Henon signals with the conventional multisine waveforms in terms of WPT performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge