Multi-armed Bandit Learning on a Graph

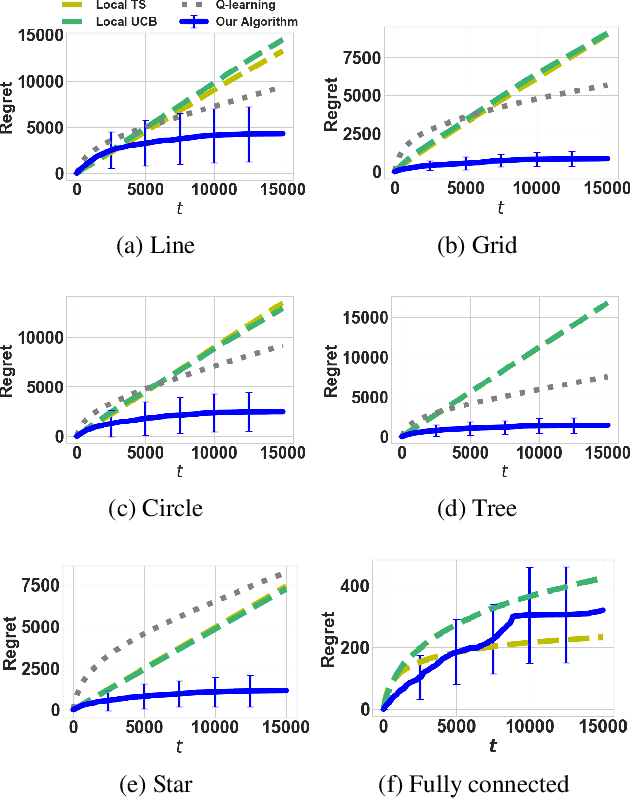
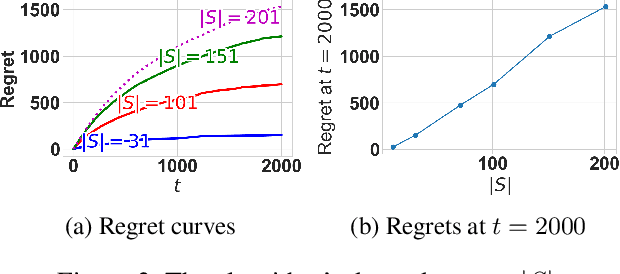
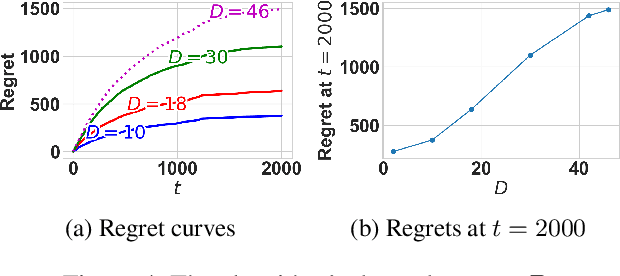
The multi-armed bandit(MAB) problem is a simple yet powerful framework that has been extensively studied in the context of decision-making under uncertainty. In many real-world applications, such as robotic applications, selecting an arm corresponds to a physical action that constrains the choices of the next available arms (actions). Motivated by this, we study an extension of MAB called the graph bandit, where an agent travels over a graph trying to maximize the reward collected from different nodes. The graph defines the freedom of the agent in selecting the next available nodes at each step. We assume the graph structure is fully available, but the reward distributions are unknown. Built upon an offline graph-based planning algorithm and the principle of optimism, we design an online learning algorithm that balances long-term exploration-exploitation using the principle of optimism. We show that our proposed algorithm achieves $O(|S|\sqrt{T}\log(T)+D|S|\log T)$ learning regret, where $|S|$ is the number of nodes and $D$ is the diameter of the graph, which is superior compared to the best-known reinforcement learning algorithms under similar settings. Numerical experiments confirm that our algorithm outperforms several benchmarks. Finally, we present a synthetic robotic application modeled by the graph bandit framework, where a robot moves on a network of rural/suburban locations to provide high-speed internet access using our proposed algorithm.