Multi-Agent Task Allocation in Complementary Teams: A Hunter and Gatherer Approach

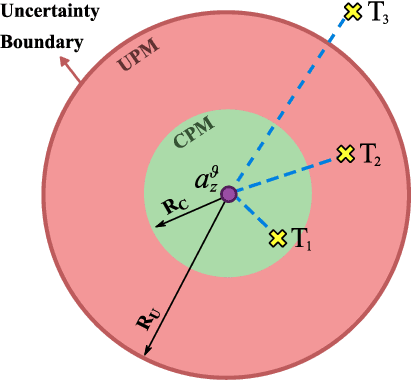
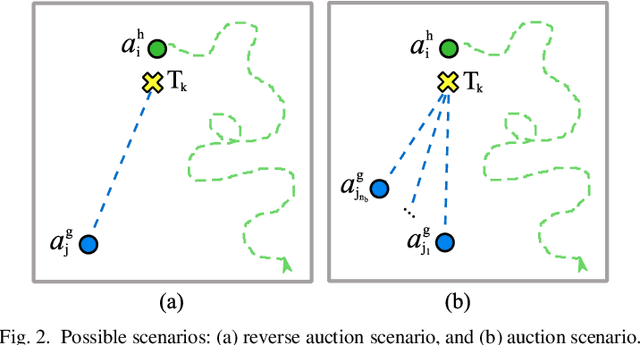
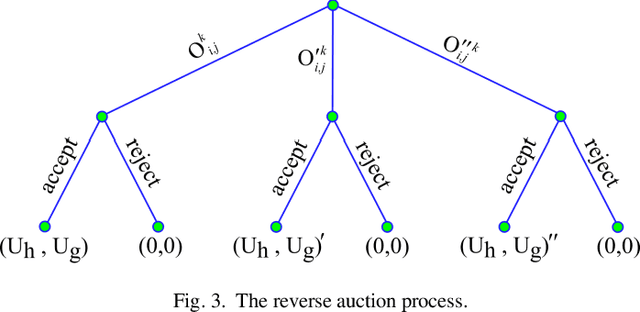
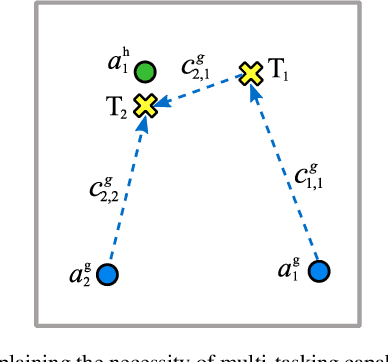
Consider a dynamic task allocation problem, where tasks are unknowingly distributed over an environment. This paper considers each task comprised of two sequential subtasks: detection and completion, where each subtask can only be carried out by a certain type of agent. We address this problem using a novel nature-inspired approach called "hunter and gatherer". The proposed method employs two complementary teams of agents: one agile in detecting (hunters) and another dexterous in completing (gatherers) the tasks. To minimize the collective cost of task accomplishments in a distributed manner, a game-theoretic solution is introduced to couple agents from complementary teams. We utilize market-based negotiation models to develop incentive-based decision-making algorithms relying on innovative notions of "certainty and uncertainty profit margins". The simulation results demonstrate that employing two complementary teams of hunters and gatherers can effectually improve the number of tasks completed by agents compared to conventional methods, while the collective cost of accomplishments is minimized. In addition, the stability and efficacy of the proposed solutions are studied using Nash equilibrium analysis and statistical analysis respectively. It is also numerically shown that the proposed solutions function fairly, i.e. for each type of agent, the overall workload is distributed equally.