Module-based regularization improves Gaussian graphical models when observing noisy data

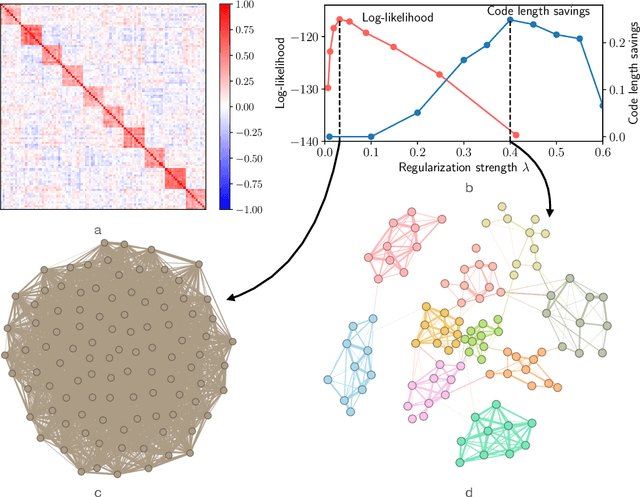
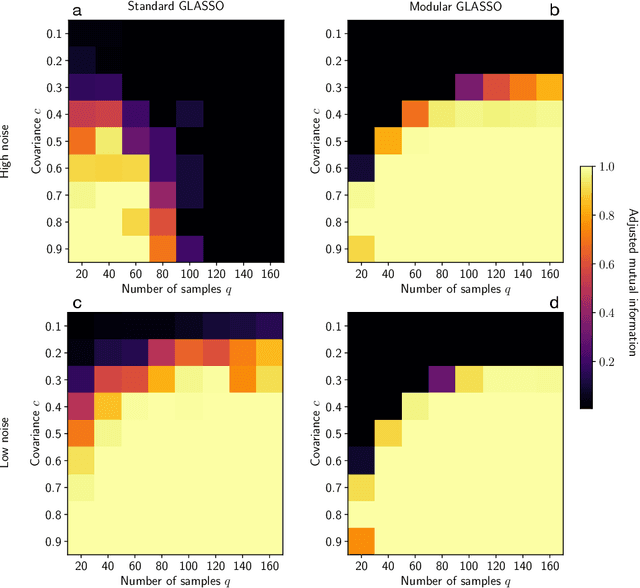
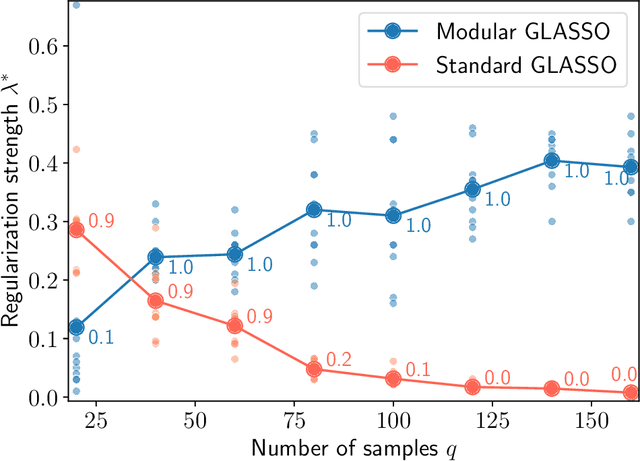
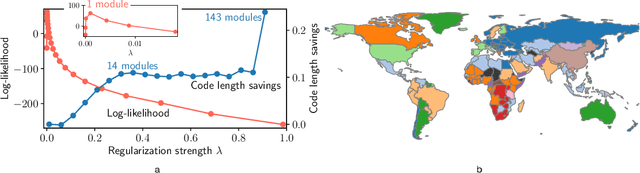
Researchers often represent relations in multi-variate correlational data using Gaussian graphical models, which require regularization to sparsify the models. Acknowledging that they often study the modular structure of the inferred network, we suggest integrating it in the cross-validation of the regularization strength to balance under- and overfitting. Using synthetic and real data, we show that this approach allows us to better recover and infer modular structure in noisy data compared with the graphical lasso, a standard approach using the Gaussian log-likelihood when cross-validating the regularization strength.