Model-free Policy Learning with Reward Gradients
Paper and Code
Mar 09, 2021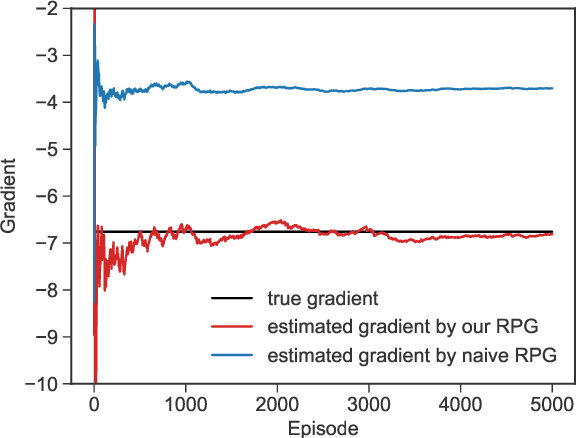
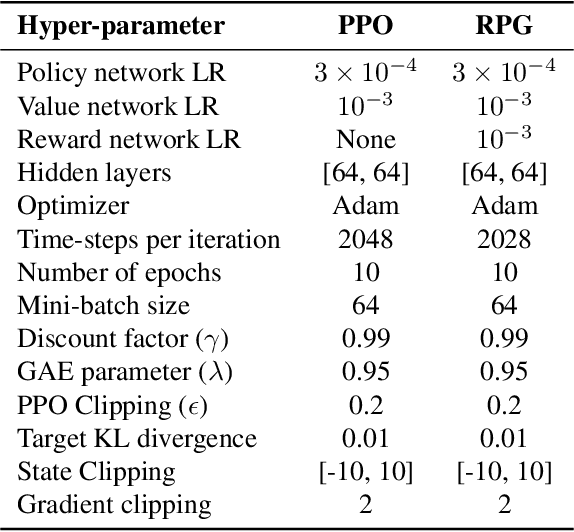
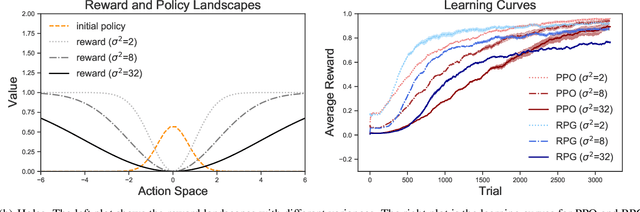
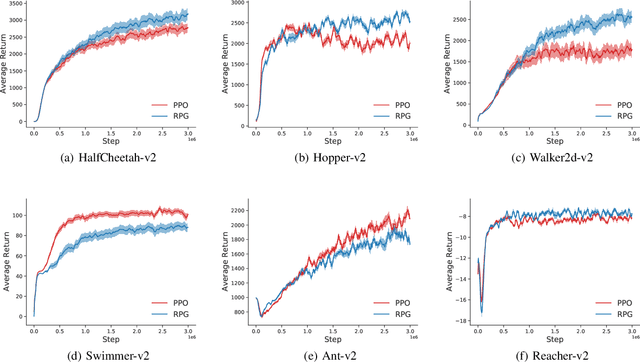
Policy gradient methods estimate the gradient of a policy objective solely based on either the likelihood ratio (LR) estimator or the reparameterization (RP) estimator for estimating gradients. Many policy gradient methods based on the LR estimator can be unified under the policy gradient theorem (Sutton et al., 2000). However, such a unifying theorem does not exist for policy gradient methods based on the RP estimator. Moreover, no existing method requires and uses both estimators beyond a trivial interpolation between them. In this paper, we provide a theoretical framework that unifies several existing policy gradient methods based on the RP estimator. Utilizing our framework, we introduce a novel strategy to compute the policy gradient that, for the first time, incorporates both the LR and RP estimators and can be unbiased only when both estimators are present. Based on this strategy, we develop a new on-policy algorithm called the Reward Policy Gradient algorithm, which is the first model-free policy gradient method to utilize reward gradients. Using an idealized environment, we show that policy gradient solely based on the RP estimator for rewards are biased even with true rewards whereas our combined estimator is not. Finally, we show that our method either performs comparably with or outperforms Proximal Policy Optimization -- an LR-based on-policy method -- on several continuous control tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge