Model-Driven Applications of Fractional Derivatives and Integrals
Paper and Code
Mar 21, 2014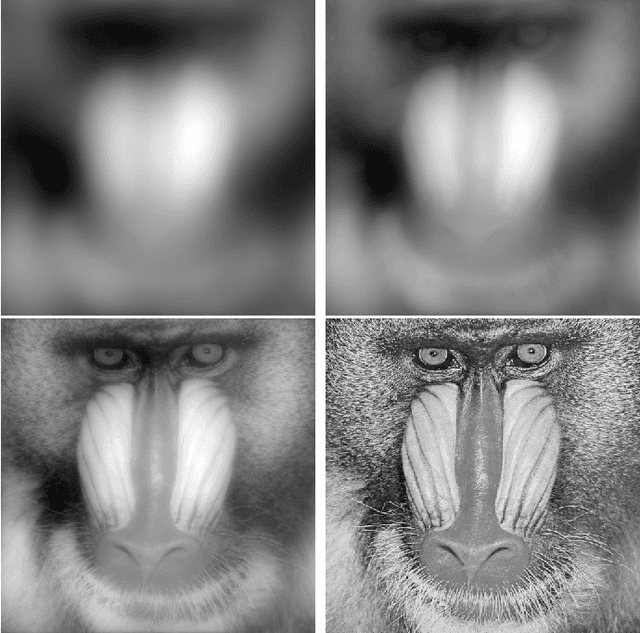

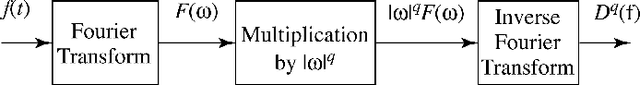
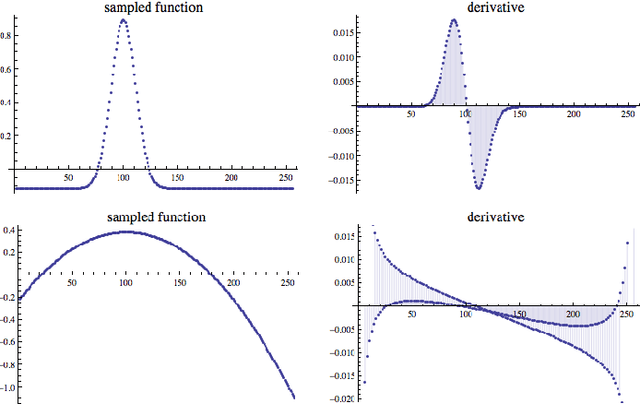
Fractional order derivatives and integrals (differintegrals) are viewed from a frequency-domain perspective using the formalism of Riesz, providing a computational tool as well as a way to interpret the operations in the frequency domain. Differintegrals provide a logical extension of current techniques, generalizing the notion of integral and differential operators and acting as kind of frequency-domain filtering that has many of the advantages of a nonlocal linear operator. Several important properties of differintegrals are presented, and sample applications are given to one- and two-dimensional signals. Computer code to carry out the computations is made available on the author's website.
* 22 pages, 10 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge