Mixed Integer Programming for Searching Maximum Quasi-Bicliques
Paper and Code
Feb 23, 2020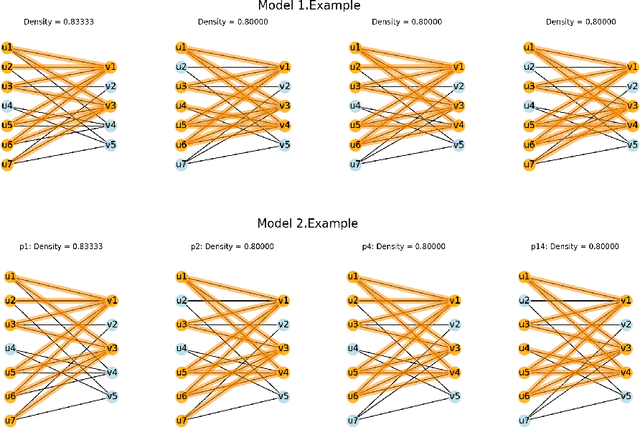
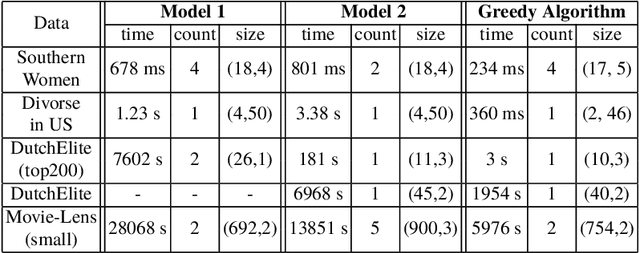
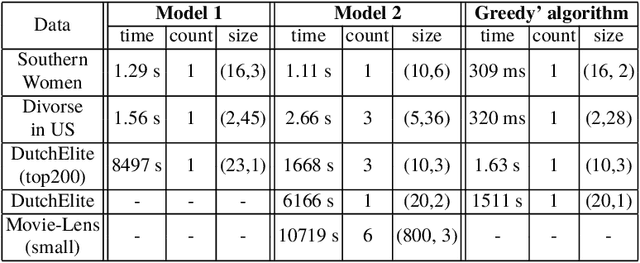
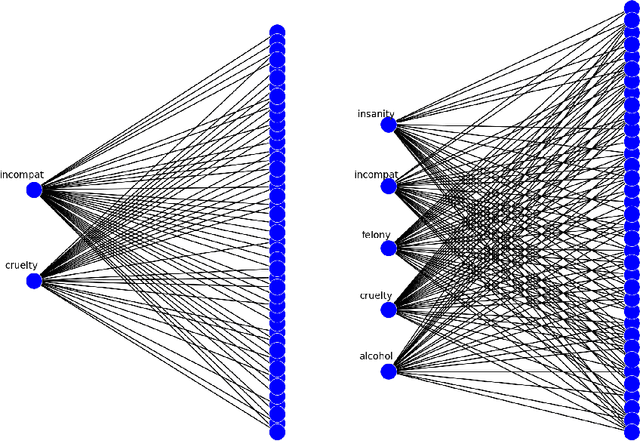
This paper is related to the problem of finding the maximal quasi-bicliques in a bipartite graph (bigraph). A quasi-biclique in the bigraph is its "almost" complete subgraph. The relaxation of completeness can be understood variously; here, we assume that the subgraph is a $\gamma$-quasi-biclique if it lacks a certain number of edges to form a biclique such that its density is at least $\gamma \in (0,1]$. For a bigraph and fixed $\gamma$, the problem of searching for the maximal quasi-biclique consists of finding a subset of vertices of the bigraph such that the induced subgraph is a quasi-biclique and its size is maximal for a given graph. Several models based on Mixed Integer Programming (MIP) to search for a quasi-biclique are proposed and tested for working efficiency. An alternative model inspired by biclustering is formulated and tested; this model simultaneously maximizes both the size of the quasi-biclique and its density, using the least-square criterion similar to the one exploited by triclustering \textsc{TriBox}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge